ABC-062-C Chocolate Bar

■■■問題■■■

縦Hブロック、横Wブロックの板チョコがあります。
すぬけ君は、この板チョコをちょうど3つのピースに分割しようとしています。
ただし、各ピースはブロックの境目に沿った長方形でなければなりません。

すぬけ君は、3つのピースの面積(ブロック数)をできるだけ均等にしようとしています。
具体的には、3つのピースの面積の最大値をSmax、最小値をSminとしたとき、
Smax-Sminを最小化しようとしています。
Smax-Sminの最小値を求めてください。

■■■入力■■■

H W

●2 <= H,W <= 10万

■■■出力■■■

Smax-Sminの最小値を出力せよ。

■■■サンプルケースのイメージ■■■

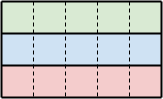
■入出力例1のイメージ■
次図のように分割すると、Smax-Smin = 5-5 = 0 となります。



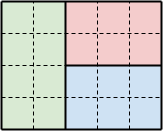
■入出力例2のイメージ■
次図のように分割すると、Smax-Smin = 8-6 = 2 となります。



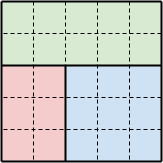
■入出力例3のイメージ■
次図のように分割すると、Smax-Smin = 10-6 = 4 となります。

C#のソース

using System;
using System.Collections.Generic;
using System.Linq;

class Program
{
    static string InputPattern = "Input1";

    static List<string> GetInputList()
    {
        var WillReturn = new List<string>();

        if (InputPattern == "Input1") {
            WillReturn.Add("3 5");
            //0
        }
        else if (InputPattern == "Input2") {
            WillReturn.Add("4 5");
            //2
        }
        else if (InputPattern == "Input3") {
            WillReturn.Add("5 5");
            //4
        }
        else if (InputPattern == "Input4") {
            WillReturn.Add("100000 2");
            //1
        }
        else if (InputPattern == "Input5") {
            WillReturn.Add("100000 100000");
            //50000
        }
        else {
            string wkStr;
            while ((wkStr = Console.ReadLine()) != null) WillReturn.Add(wkStr);
        }
        return WillReturn;
    }

    static void Main()
    {
        List<string> InputList = GetInputList();
        long[] wkArr = InputList[0].Split(' ').Select(X => long.Parse(X)).ToArray();
        long H = wkArr[0];
        long W = wkArr[1];

        long AnswerKouho1 = Solve(H, W);
        long AnswerKouho2 = Solve(W, H);
        Console.WriteLine(Math.Min(AnswerKouho1, AnswerKouho2));
    }

    static long Solve(long pH, long pW)
    {
        long WillReturn = long.MaxValue;
        for (int LoopAW = 1; LoopAW <= pW - 1; LoopAW++) {
            long MensekiA = LoopAW * pH;

            long RestW = pW - LoopAW;

            //残りの取り方1
            long MensekiB = (RestW / 2) * pH;
            long MensekiC = Div2Kiriage(RestW) * pH;
            long wkMinMaxDiff = DeriveMinMaxDiff(MensekiA, MensekiB, MensekiC);
            if (WillReturn > wkMinMaxDiff)
                WillReturn = wkMinMaxDiff;

            //残りの取り方2
            MensekiB = RestW * (pH / 2);
            MensekiC = RestW * Div2Kiriage(pH);
            wkMinMaxDiff = DeriveMinMaxDiff(MensekiA, MensekiB, MensekiC);
            if (WillReturn > wkMinMaxDiff)
                WillReturn = wkMinMaxDiff;
        }
        return WillReturn;
    }

    //2で割って端数切り上げ
    static long Div2Kiriage(long pVal)
    {
        long WillReturn = pVal / 2;
        if (pVal % 2 > 0) WillReturn++;
        return WillReturn;
    }

    //最大面積と最小面積の差を返す
    static long DeriveMinMaxDiff(long pA, long pB, long pC)
    {
        long MinVal = Math.Min(Math.Min(pA, pB), pC);
        long MaxVal = Math.Max(Math.Max(pA, pB), pC);
        return MaxVal - MinVal;
    }
}

解説

ABCの順に分けるとして、
分け方は、下記の4通りです。
AABBB
AABBB
AACCC
AACCC

AABCC
AABCC
AABCC
AABCC

AAAAA
AAAAA
BBBBB
CCCCC

AAAAA
AAAAA
BBCCC
BBCCC

90度回転させたケースを除外すると、下記の2通りです。
AABBB
AABBB
AACCC
AACCC

AABCC
AABCC
AABCC
AABCC

後は、長方形Aの決め方を全探索し、
残りの長方形Bと長方形Cは、小さいほうの長方形の面積をなるべく大きくし
大きいほうの長方形の面積をなるべく小さくするのが最適なことをふまえて、
残りの長方形を決定してます。