Problem114 ブロックを離して一列に敷き詰める方法の数

問題

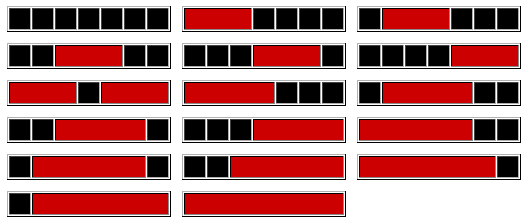
長さ 7 ユニットからなる 1 列上に, 最低 3 ユニットの長さを持つ赤ブロックが置かれている.
ただしどの赤ブロック同士も, 少なくとも 1 ユニットの黒い正方形が間にある
(赤ブロックは長さが異なってもよい). これを敷き詰める方法は, ちょうど 17 通りある.


50 ユニットの長さの 1 列を敷き詰める方法は何通りあるか.

注意: 上の例では起こりえないが, 通常はブロックの大きさが複数混ざっていてもよい.
例えば, 8 ユニットの長さの 1 列では, 赤(3), 黒(1), 赤(4) を使うことができる.

ソース

using System;
using System.Collections.Generic;

class Program
{
    //const int Units = 7;
    const int Units = 50;

    //事前に組み合わせ数を求めておく、残マス数
    const int DerivedRestCnt = Units / 2;

    static void Main()
    {
        var sw = System.Diagnostics.Stopwatch.StartNew();

        for (int I = 1; I <= DerivedRestCnt; I++) {
            DeriveCaseCntFromBlack(I, true);
            DeriveCaseCntFromBlack(I, false);
        }

        var Stk = new Stack<string>();

        for (int I = 1; I <= Units; I++) Stk.Push(new string('B', I));
        for (int I = 3; I <= Units; I++) Stk.Push(new string('R', I));

        long AnsCnt = 0;

        while (Stk.Count > 0) {
            string Popped = Stk.Pop();

            if (Popped.Length == Units) {
                AnsCnt++;
                continue;
            }

            bool IsNextBlack = Popped.EndsWith("R");
            int RestUnits = Units - Popped.Length; //残マス数

            if (RestUnits <= DerivedRestCnt) {
                if (IsNextBlack) AnsCnt += CaseCntStartBlackDict[RestUnits];
                else AnsCnt += CaseCntStartRedDict[RestUnits];
                continue;
            }

            if (IsNextBlack) {
                for (int I = 1; I <= Units - Popped.Length; I++)
                    Stk.Push(Popped + new string('B', I));
            }
            else {
                for (int I = 3; I <= Units - Popped.Length; I++)
                    Stk.Push(Popped + new string('R', I));
            }
        }
        Console.WriteLine("経過時間={0},解の数={1}", sw.Elapsed, AnsCnt);
    }

    //残りNマスでの組み合わせ数を求める
    static Dictionary<int, long> CaseCntStartBlackDict = new Dictionary<int, long>();
    static Dictionary<int, long> CaseCntStartRedDict = new Dictionary<int, long>();
    static void DeriveCaseCntFromBlack(int pUnits, bool IsStartBlack)
    {
        var Stk = new Stack<string>();
        if (IsStartBlack) {
            for (int I = 1; I <= pUnits; I++) Stk.Push(new string('B', I));
        }
        else {
            for (int I = 3; I <= pUnits; I++) Stk.Push(new string('R', I));
        }

        long CombiCnt = 0;

        while (Stk.Count > 0) {
            string Popped = Stk.Pop();

            if (Popped.Length == pUnits) {
                CombiCnt++;
                continue;
            }
            if (Popped.EndsWith("R")) {
                for (int I = 1; I <= pUnits - Popped.Length; I++)
                    Stk.Push(Popped + new string('B', I));
            }
            else {
                for (int I = 3; I <= pUnits - Popped.Length; I++)
                    Stk.Push(Popped + new string('R', I));
            }
        }
        if (IsStartBlack) CaseCntStartBlackDict[pUnits] = CombiCnt;
        else CaseCntStartRedDict[pUnits] = CombiCnt;
    }
}

実行結果

経過時間=00:00:04.3644245,解の数=16475640049

解説

事前に組み合わせ数を求めておくことで、計算量を減らしてます。

深さ優先探索ではなく動的計画法で解くこともできます。