Cマガ電脳クラブ(第014回) くずしてください！

問題

千円札を硬貨に両替することを考える。
たとえば、2枚の硬貨に両替するには、1通りの方法 (500円×2枚) しかないが、11枚だと3通りの方法がある。
　・100円玉×9枚と50円玉×2枚
　・500円玉×1枚と50円玉×10枚
　・500円玉×1枚と100円玉×4枚と50円玉×1枚と10円玉×5枚
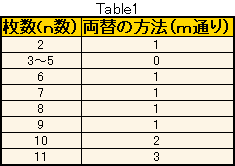
もちろん、絶対に両替できない枚数もある (例：3枚) 。Table1に2〜11枚の両替方法の数を示す。

ではここで問題。「千円札をn枚の高価に両替するには、m通りの方法がある」とした場合に、
mが最大になるのはnがいくつのときだろうか。

現在の日本で一般に流通している硬貨は、500円玉、100円玉、50円玉、10円玉、5円玉、1円玉である。念のため。

ソース

using System;
using System.Collections.Generic;
using System.Linq;

class Program
{
    struct JyoutaiDef
    {
        internal int CurrP;
        internal int Maisuu;
        internal int SumYen;
        internal string Keiro;
    }

    static void Main()
    {
        var sw = System.Diagnostics.Stopwatch.StartNew();
        var stk = new Stack<JyoutaiDef>();
        JyoutaiDef WillPush;

        int[] CoinArr = { 1, 5, 10, 50, 100, 500 };

        for (int P = 0; P <= CoinArr.GetUpperBound(0); P++) {
            WillPush.CurrP = P;
            WillPush.Maisuu = 1;
            WillPush.SumYen = CoinArr[P];
            WillPush.Keiro = CoinArr[P].ToString() + ",";
            stk.Push(WillPush);
        }

        var ResultDict = new Dictionary<int, int>();
        int CombiCnt = 0;

        while (stk.Count > 0) {
            JyoutaiDef Popped = stk.Pop();

            if (Popped.SumYen == 1000) {
                if (++CombiCnt <= 15) { //最初の15個のみを表示
                    Console.WriteLine("1000円になる{0}個目の組み合わせを発見。{1}",
                        CombiCnt, Popped.Keiro);
                }

                if (ResultDict.ContainsKey(Popped.Maisuu))
                    ResultDict[Popped.Maisuu]++;
                else ResultDict[Popped.Maisuu] = 1;

                continue;
            }

            for (int P = Popped.CurrP; P <= CoinArr.GetUpperBound(0); P++) {
                WillPush.CurrP = P;
                WillPush.Maisuu = Popped.Maisuu + 1;
                WillPush.SumYen = Popped.SumYen + CoinArr[P];
                if (WillPush.SumYen > 1000) break;
                WillPush.Keiro = Popped.Keiro + CoinArr[P].ToString() + ",";
                stk.Push(WillPush);
            }
        }

        foreach (var AnyPair in ResultDict.OrderBy(X => X.Value).ThenBy(X => X.Key)) {
            Console.WriteLine("{0}枚に両替する方法は{1}通り", AnyPair.Key, AnyPair.Value);
        }
        Console.WriteLine("経過時間={0}", sw.Elapsed);
    }
}

実行結果

省略
142枚に両替する方法は788通り
152枚に両替する方法は788通り
143枚に両替する方法は789通り
151枚に両替する方法は789通り
147枚に両替する方法は790通り
経過時間=00:01:30.6645283

解説

枚数ごとの組み合わせの数を、Dictionaryジェネリックで管理してます。