Cマガ電脳クラブ(第041回) Robinson Roulette

問題

Milton Bradley社製のRobinson Rouletteというコンピュータ向きのパズルをみつけたので紹介しよう。

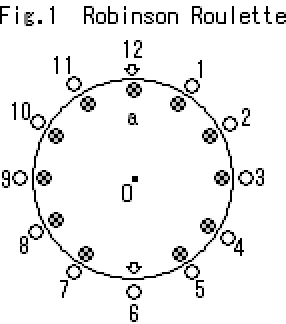
時計の文字盤のように番号をつけた11個の穴と矢印 (これは12時の位置) が円形に並んだ台がある。
その内側に、やはり11個の穴と1個の矢印が円形に並んだ0を中心に回転する円盤がついている。
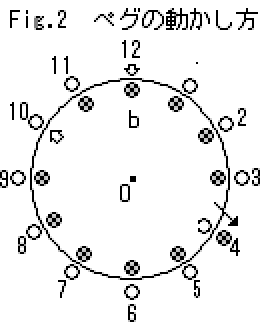
Fig.2はスタートの状態で、内側の円盤の穴には11本のペグ (図の×印) が立っている。
　(1) 12番の矢印のすぐ下にきている円盤状のペグ (Fig.1のａ) をつまむ
　(2) つまんだまま、外側の空いている穴の、どれか1つの横まで内側の円盤を回転する
　(3) 内側から外側の穴へ、そのペグを移す
この(1)〜(3)の操作を繰り返す。
たとえばFig.1のペグ(a)をFig.2のように4番の穴に移動したとすると、次の(1)の操作ではbをつまむことになる。
この操作を11回行って、すべてのペグを外側のダイヤルに移動するのが目的だ。

大事なことは、あるペグを移動したときに、
次に使うペグが12番の矢印のところにないとあとが続かないということだ
(たとえば、第2手目のbは2番または8番の穴にペグを持っていけない)。

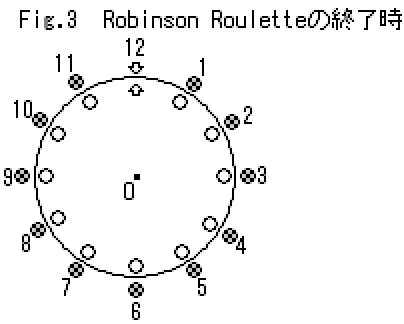
スタート (Fig.1) の状態から上記(1)〜(3)の操作を11回繰り返してゴール(Fig.3)の状態にするには、
何通りの方法があるだろうか。
なお、11個すべてのペグを外側に移動し終えたときには、
Fig.3のように円盤状の矢印は12番の矢印のところに位置しなければならない。
解答を一例だけ示そう。数はペグの移動先の穴の番号である。
 1、2、4、7、8、10、3、6、11、5、9

     

ソース

using System;
using System.Collections.Generic;

class Program
{
    const int UB = 12 - 1;

    struct JyoutaiDef
    {
        internal char[] AnaArr; //外側の穴の配列 (回転しない)
        internal List<char[]> AnaArrLog;

        internal char[] PegArr; //内側のペグの配列 (回転する)
        internal List<char[]> PegArrLog;

        internal List<int> DestLog;
    }

    static void Main()
    {
        var sw = System.Diagnostics.Stopwatch.StartNew();

        var stk = new Stack<JyoutaiDef>();
        JyoutaiDef WillPush;

        WillPush.AnaArr = new char[UB + 1];
        WillPush.AnaArr[0] = '↓';
        for (int I = 1; I <= UB; I++) {
            WillPush.AnaArr[I] = '穴';
        }
        WillPush.AnaArrLog = new List<char[]>() { WillPush.AnaArr };

        WillPush.PegArr = new char[UB + 1];
        for (int I = 0; I <= UB; I++) {
            WillPush.PegArr[I] = '●';
            if (I == 6) WillPush.PegArr[I] = '↑';
        }
        WillPush.PegArrLog = new List<char[]>() { WillPush.PegArr };

        WillPush.DestLog = new List<int>();
        stk.Push(WillPush);

        int AnswerCnt = 0;

        while (stk.Count > 0) {
            JyoutaiDef Popped = stk.Pop();

            //クリア判定
            if (IsClear(Popped.PegArr)) {
                AnswerCnt++;

                if (AnswerCnt == 1) {
                    Console.WriteLine("解{0}を発見", AnswerCnt);
                    for (int I = 0; I <= Popped.AnaArrLog.Count - 1; I++) {
                        if (I > 0) Console.WriteLine("{0}にペグを移動", Popped.DestLog[I - 1]);
                        PrintBan(Popped.AnaArrLog[I], Popped.PegArrLog[I]);
                        Console.WriteLine();
                    }
                }
                continue;
            }

            if (Popped.PegArr[0] != '●') continue;

            //ペグの移動処理
            for (int I = 1; I <= UB; I++) {
                if (Popped.AnaArr[I] != '穴') continue;

                WillPush.AnaArr = (char[])Popped.AnaArr.Clone();
                WillPush.AnaArr[I] = '●';
                WillPush.AnaArrLog = new List<char[]>(Popped.AnaArrLog) { WillPush.AnaArr };

                WillPush.PegArr = (char[])Popped.PegArr.Clone();
                //回転処理
                for (int SrcInd = 0; SrcInd <= UB; SrcInd++) {
                    int DestInd = SrcInd + I;
                    if (DestInd > UB) DestInd -= (UB + 1);
                    WillPush.PegArr[DestInd] = Popped.PegArr[SrcInd];
                }

                WillPush.PegArr[I] = '穴';
                WillPush.PegArrLog = new List<char[]>(Popped.PegArrLog) { WillPush.PegArr };

                WillPush.DestLog = new List<int>(Popped.DestLog) { I };
                stk.Push(WillPush);
            }
        }
        Console.WriteLine("解は{0}通り", AnswerCnt);
    }

    //クリア判定
    static bool IsClear(char[] pPegArr)
    {
        if (pPegArr[0] != '↑') return false;
        for (int I = 1; I <= UB; I++) {
            if (pPegArr[I] != '穴') return false;
        }
        return true;
    }

    //盤面を表示
    static void PrintBan(char[] pAnaArr, char[] pPegArr)
    {
        var sb = new System.Text.StringBuilder();
        Array.ForEach(pAnaArr, X => sb.Append(X));
        sb.AppendLine();
        Array.ForEach(pPegArr, X => sb.Append(X));
        Console.WriteLine(sb.ToString());
    }
}

実行結果

解1を発見
↓穴穴穴穴穴穴穴穴穴穴穴
●●●●●●↑●●●●●

11にペグを移動
↓穴穴穴穴穴穴穴穴穴穴●
●●●●●↑●●●●●穴

10にペグを移動
↓穴穴穴穴穴穴穴穴穴●●
●●●↑●●●●●穴穴●

8にペグを移動
↓穴穴穴穴穴穴穴●穴●●
●●●●●穴穴●穴●●↑

5にペグを移動
↓穴穴穴穴●穴穴●穴●●
●穴●●↑穴●●●●穴穴

9にペグを移動
↓穴穴穴穴●穴穴●●●●
●↑穴●●●●穴穴穴穴●

6にペグを移動
↓穴穴穴穴●●穴●●●●
●穴穴穴穴●穴↑穴●●●

1にペグを移動
↓●穴穴穴●●穴●●●●
●穴穴穴穴穴●穴↑穴●●

2にペグを移動
↓●●穴穴●●穴●●●●
●●穴穴穴穴穴穴●穴↑穴

4にペグを移動
↓●●穴●●●穴●●●●
●穴↑穴穴●穴穴穴穴穴穴

7にペグを移動
↓●●穴●●●●●●●●
●穴穴穴穴穴穴穴穴↑穴穴

3にペグを移動
↓●●●●●●●●●●●
↑穴穴穴穴穴穴穴穴穴穴穴

解は3856通り

解説

深さ優先探索で解いてます。

Robinson Roulette