Cマガ電脳クラブ(第050回) 上下反転

問題

3×3の盤にFig.1のように将棋の駒を置く。
駒を移動して、Fig.2のように上下反転の配置にするのに、最少手数は何手だろうか。これが今回の問題である。

それぞれの駒が移動できる方向を、Fig.3に示してある。なお、「銅」は中将棋に使われる銅将である。
3×3の盤の外に出たり、すでに駒があるマスに移動することは許されない。

     

ソース

using System;
using System.Collections.Generic;

class Program
{
    const int UB = 3 - 1;

    struct JyoutaiDef
    {
        internal int Level;
        internal char[,] BanArr;
        internal List<char[,]> BanArrLogList;
    }

    static void Main()
    {
        char[,] wkArr = {{'銅','飛','銅'},
                         {'銅',' ' ,'銅'},
                         {'歩','銀','歩'}};

        var Stk = new Stack<JyoutaiDef>();
        JyoutaiDef WillPush;

        WillPush.Level = 0;
        WillPush.BanArr = new char[UB + 1, UB + 1];
        for (int X = 0; X <= UB; X++) {
            for (int Y = 0; Y <= UB; Y++) {
                WillPush.BanArr[X, Y] = wkArr[Y, X];
            }
        }
        WillPush.BanArrLogList = new List<char[,]>() { WillPush.BanArr };
        Stk.Push(WillPush);

        int AnswerMinLevel = int.MaxValue;

        //盤面に対する最少手数のDict
        var SortedMinTesuuDict = new SortedDictionary<uint, int>();

        while (Stk.Count > 0) {
            JyoutaiDef Popped = Stk.Pop();

            if (Popped.Level > AnswerMinLevel) continue;

            if (IsGoal(Popped.BanArr)) {
                AnswerMinLevel = Popped.Level;
                Console.WriteLine("{0}手の解候補を発見", Popped.Level);

                for (int I = 0; I <= Popped.BanArrLogList.Count - 1; I++) {
                    Console.WriteLine("{0}手目", I);
                    PrintBan(Popped.BanArrLogList[I]);
                }
                continue;
            }

            //空白マスを探す
            int SpaceX = -1, SpaceY = -1;
            Action SearchSpaceMasu = () =>
            {
                for (int X = 0; X <= UB; X++) {
                    for (int Y = 0; Y <= UB; Y++) {
                        if (Popped.BanArr[X, Y] == ' ') {
                            SpaceX = X; SpaceY = Y;
                            return;
                        }
                    }
                }
            };
            SearchSpaceMasu();

            WillPush.Level = Popped.Level + 1;
            foreach (PointDef EachPoint in DeriveFromMasuList(Popped.BanArr, SpaceX, SpaceY)) {
                WillPush.BanArr = (char[,])Popped.BanArr.Clone();
                char MoveKoma = Popped.BanArr[EachPoint.X, EachPoint.Y];
                WillPush.BanArr[SpaceX, SpaceY] = MoveKoma;
                WillPush.BanArr[EachPoint.X, EachPoint.Y] = ' ';

                //当該盤面に、少ない手数か等しい手数で、到達済なら枝切り
                uint BanUint = BanToUint(WillPush.BanArr);
                int MinTesuu;
                if (SortedMinTesuuDict.TryGetValue(BanUint, out MinTesuu)) {
                    if (MinTesuu <= WillPush.Level) continue;
                }
                SortedMinTesuuDict[BanUint] = WillPush.Level;

                WillPush.BanArrLogList = new List<char[,]>(Popped.BanArrLogList) { WillPush.BanArr };
                Stk.Push(WillPush);
            }
        }
    }

    struct PointDef
    {
        internal int X;
        internal int Y;
    }

    //空白マスを引数として、その空白に移動可能な駒の座標のリストを返す
    static List<PointDef> DeriveFromMasuList(char[,] pBanArr, int pSpaceX, int pSpaceY)
    {
        var WillReturnList = new List<PointDef>();

        //移動可能な駒と、移動元座標を引数として、
        //条件を満たしてたらAdd
        Action<char, int, int> CheckAndAdd = (pKoma, pFromX, pFromY) =>
        {
            if (pFromX < 0 || UB < pFromX) return;
            if (pFromY < 0 || UB < pFromY) return;
            if (pBanArr[pFromX, pFromY] == pKoma)
                WillReturnList.Add(new PointDef() { X = pFromX, Y = pFromY });
        };

        //空白の上の駒が移動
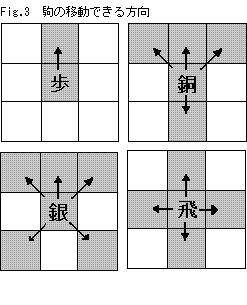
        CheckAndAdd('銅', pSpaceX, pSpaceY - 1);
        CheckAndAdd('飛', pSpaceX, pSpaceY - 1);

        //空白の右上の駒が移動
        CheckAndAdd('銀', pSpaceX + 1, pSpaceY - 1);

        //空白の右の駒が移動
        CheckAndAdd('飛', pSpaceX + 1, pSpaceY);

        //空白の右下の駒が移動
        CheckAndAdd('銅', pSpaceX + 1, pSpaceY + 1);
        CheckAndAdd('銀', pSpaceX + 1, pSpaceY + 1);

        //空白の下の駒が移動
        CheckAndAdd('歩', pSpaceX, pSpaceY + 1);
        CheckAndAdd('銅', pSpaceX, pSpaceY + 1);
        CheckAndAdd('銀', pSpaceX, pSpaceY + 1);
        CheckAndAdd('飛', pSpaceX, pSpaceY + 1);

        //空白の左下の駒が移動
        CheckAndAdd('銅', pSpaceX - 1, pSpaceY + 1);
        CheckAndAdd('銀', pSpaceX - 1, pSpaceY + 1);

        //空白の左の駒が移動
        CheckAndAdd('飛', pSpaceX - 1, pSpaceY);

        //空白の左上の駒が移動
        CheckAndAdd('銀', pSpaceX - 1, pSpaceY - 1);

        return WillReturnList;
    }

    //ゴールに到達したかを判定
    static bool IsGoal(char[,] pBanArr)
    {
        char[,] GoalArr = new char[,] {{'歩','銀','歩'},
                                       {'銅',' ' ,'銅'},
                                       {'銅','飛','銅'}};
        for (int X = 0; X <= UB; X++) {
            for (int Y = 0; Y <= UB; Y++) {
                if (pBanArr[X, Y] != GoalArr[Y, X])
                    return false;
            }
        }
        return true;
    }

    //盤面を符号なしInt型で表現
    static uint BanToUint(char[,] pBanArr)
    {
        var sb = new System.Text.StringBuilder();
        for (int X = 0; X <= UB; X++) {
            for (int Y = 0; Y <= UB; Y++) {
                if (pBanArr[X, Y] == '歩') sb.Append(1);
                else if (pBanArr[X, Y] == '銅') sb.Append(2);
                else if (pBanArr[X, Y] == '銀') sb.Append(3);
                else if (pBanArr[X, Y] == '飛') sb.Append(4);
                else sb.Append(0);
            }
        }
        return Convert.ToUInt32(sb.ToString(), 8);
    }

    //盤面を表示
    static void PrintBan(char[,] pBanArr)
    {
        var sb = new System.Text.StringBuilder();
        for (int Y = 0; Y <= UB; Y++) {
            for (int X = 0; X <= UB; X++) {
                if (pBanArr[X, Y] == ' ') sb.Append("  ");
                else sb.Append(pBanArr[X, Y]);
            }
            sb.AppendLine();
        }
        Console.WriteLine(sb.ToString());
    }
}

実行結果

省略
123手目
歩銀歩
銅  飛
銅銅銅

124手目
歩銀歩
銅飛
銅銅銅

125手目
歩銀歩
銅飛銅
銅  銅

126手目
歩銀歩
銅  銅
銅飛銅

解説

反復深化深さ優先探索や、双方向探索も考えましたが、
深さ優先探索で、十分な速度で解けました。