長さ1の棒、2の棒、・・・、Nの棒を順につなげて輪を作る。 長さNの棒と1の棒もつなげるワケだ。 つなぎ目を曲げるか伸ばすかは自由にできるが、棒の途中では曲げられない。 N=9の時にはFig.1のように、正三角形を作ることができる。 これを「長さ9、9から3、4から6、7から8」と表す事にする。 さて、N=1から1000の範囲で、このような正三角形の組をすべて見つけてほしい。 ひとつのNで複数組の三角形ができる可能性もお忘れなく。 Fig.1 トライアングル (N=9のとき)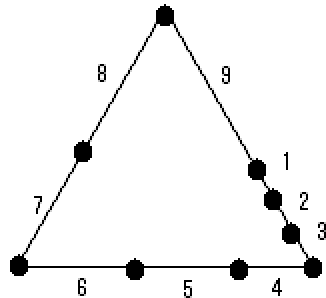
長さ1の棒、2の棒、・・・、Nの棒を順につなげて輪を作る。 長さNの棒と1の棒もつなげるワケだ。 つなぎ目を曲げるか伸ばすかは自由にできるが、棒の途中では曲げられない。 N=9の時にはFig.1のように、正三角形を作ることができる。 これを「長さ9、9から3、4から6、7から8」と表す事にする。 さて、N=1から1000の範囲で、このような正三角形の組をすべて見つけてほしい。 ひとつのNで複数組の三角形ができる可能性もお忘れなく。 Fig.1 トライアングル (N=9のとき)
using System;
using System.Collections.Generic;
class Program
{
static void Main()
{
int AnswerCnt = 0;
for (int N = 1; N <= 1000; N++) {
//和が3の倍数でない場合は対象外
int SumHenLength = (N * (N + 1)) / 2;
if (SumHenLength % 3 != 0) continue;
//チェック済の正三角形の始点のSet
var ShitenSet = new HashSet<int>();
//正三角形の始点のループ
for (int Shiten = 1; Shiten <= N; Shiten++) {
bool WillContinue = false;
var AnswerLengthList = new List<int>();
int CurrHenLength = 0;
Action<int> EachLengthSyori = (pEachLength) =>
{
if (CurrHenLength == 0) {
if (ShitenSet.Add(pEachLength) == false) {
WillContinue = true; return;
}
AnswerLengthList.Add(pEachLength);
}
CurrHenLength += pEachLength;
if (CurrHenLength == SumHenLength / 3) {
AnswerLengthList.Add(pEachLength);
CurrHenLength = 0;
}
else if (CurrHenLength > SumHenLength / 3) {
WillContinue = true;
}
};
for (int I = Shiten; I <= N; I++) {
EachLengthSyori(I);
if (WillContinue) break;
}
if (WillContinue) continue;
for (int I = 1; I < Shiten; I++) {
EachLengthSyori(I);
if (WillContinue) break;
}
if (WillContinue) continue;
if (AnswerLengthList.Count == 6) {
Console.WriteLine("解{0}", ++AnswerCnt);
Console.Write("長さ{0},", N);
for (int I = 0; I <= AnswerLengthList.Count - 1; I++) {
if (I % 2 == 0) Console.Write("{0}から", AnswerLengthList[I]);
else Console.Write("{0},", AnswerLengthList[I]);
}
Console.WriteLine();
}
}
}
}
}
解1 長さ9,4から6,7から8,9から3, 解2 長さ90,16から54,55から75,76から15, 解3 長さ125,3から72,73から102,103から2, 解4 長さ125,58から92,93から117,118から57, 解5 長さ153,52から102,103から135,136から51, 解6 長さ189,16から110,111から155,156から15, 解7 長さ440,25から255,256から360,361から24, 解8 長さ819,57から476,477から671,672から56, 解9 長さ989,165から594,595から824,825から164,
チェック済の正三角形の始点をHashSetで管理してます。