Cマガ電脳クラブ(第084回) ダイスインスタントインサニティー

問題

サイコロの目の付け方には、「対面の目を足すと7になる」というルールがある。
このルールを無視することにすると、目の付け方の違うサイコロが30種類作れる。

ところで、インスタントインサニティーというパズルがある。
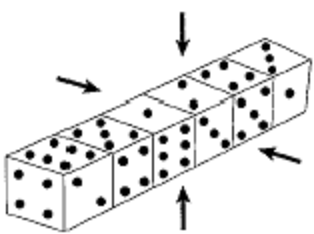
与えられた6個のサイコロをFig.1のように一直線に並べる。
このとき、六つの目が並んだ面が4面できるが (Fig.Aの矢印) 、
それぞれの面に1〜6までの目がすべて登場するように並べる、
というものだ (サイコロの順番を入れ換えたものは別解とはしない)。

このパズルの「解の数」は与えられる6個によって変わってくるが、
これが少なければ少ないほど難しいといえる。

ではここで問題。与えられる6個をうまく選ぶことで、
どこまでこのパズルの「解の数」を減らすことができるだろうか。
その「解の数」を答えていただきたい。ただし、サイコロは前述の30個から選ぶとし、同じものは使わない。

Fig.A 6個のサイコロ

ソース

using System;
using System.Collections.Generic;
using System.Linq;

class Program
{
    static Dictionary<int, List<int[]>> Use4MenArrListDict =
        new Dictionary<int, List<int[]>>();

    const int UB = 3;

    struct JyoutaiDef1
    {
        internal int CurrP;
        internal int Level;
        internal List<int[]> DiceHaitiList; //要素数が4の配列のList
        internal string UsedDiceIndStr; //使用したダイスの添字
    }

    static void Main()
    {
        var sw = System.Diagnostics.Stopwatch.StartNew();

        //この展開図と配列の添字を対応させて、30個のダイスの展開図を定義
        // 0
        //123
        // 4
        // 5

        List<int[]> wk6MenArrList = Derive6MenArrList();
        for (int I = 0; I <= wk6MenArrList.Count - 1; I++) {
            Console.Write("ダイス番号{0}の展開図は、", I);
            Array.ForEach(wk6MenArrList[I], X => Console.Write(X));
            Console.WriteLine();
        }

        for (int I = 0; I <= wk6MenArrList.Count - 1; I++) {
            //1つのダイスの、使用する4面の候補を求める
            Use4MenArrListDict[I] = DeriveUse4MenArrList(wk6MenArrList[I]);
        }

        var stk = new Stack<JyoutaiDef1>();
        JyoutaiDef1 WillPush;
        WillPush.Level = 1;
        for (int I = 0; I <= Use4MenArrListDict[0].Count - 1; I++) {
            //回転解の除外で1つめのダイスの配置は、24通りではなく3通りとする
            if (I != 0 && I != 8 && I != 16) continue;

            WillPush.CurrP = 0;
            WillPush.DiceHaitiList = new List<int[]>() { Use4MenArrListDict[0][I] };
            WillPush.UsedDiceIndStr = "0";
            stk.Push(WillPush);
        }

        var AnswerCntDict = new Dictionary<string, int>();
        int PopCnt = 0;

        while (stk.Count > 0) {
            JyoutaiDef1 Popped = stk.Pop();
            if (++PopCnt % 100000 == 0) {
                Console.WriteLine("{0}回目のPop内容={1}。経過時間={2}",
                    PopCnt, Popped.UsedDiceIndStr, sw.Elapsed);
            }

            //解判定
            if (Popped.Level == 6) {
                string KeyStr = Popped.UsedDiceIndStr;
                if (AnswerCntDict.ContainsKey(KeyStr))
                    AnswerCntDict[KeyStr]++;
                else AnswerCntDict[KeyStr] = 1;

                continue;
            }

            foreach (var EachPair in Use4MenArrListDict) {
                if (EachPair.Key <= Popped.CurrP) continue;
                List<int[]> wk4MenArrList = EachPair.Value;

                for (int I = 0; I <= wk4MenArrList.Count - 1; I++) {
                    WillPush.CurrP = EachPair.Key;
                    WillPush.Level = Popped.Level + 1;
                    WillPush.DiceHaitiList = new List<int[]>(Popped.DiceHaitiList);
                    WillPush.DiceHaitiList.Add(wk4MenArrList[I]);

                    //枝切り
                    if (IsValid(WillPush.DiceHaitiList) == false) continue;

                    WillPush.UsedDiceIndStr = Popped.UsedDiceIndStr + "," + EachPair.Key.ToString();
                    stk.Push(WillPush);
                }
            }
        }

        var AnswerPair = AnswerCntDict.OrderBy(X => X.Value).First();
        Console.WriteLine("解となるダイス番号リストは{0}で、{1}通り",
            AnswerPair.Key, AnswerPair.Value);
    }

    //有効な状態かを返す
    static bool IsValid(List<int[]> pDiceHaitiList)
    {
        for (int I = 0; I <= UB; I++) {
            var wkHashSet = new HashSet<int>();
            for (int J = 0; J <= pDiceHaitiList.Count - 1; J++) {
                if (wkHashSet.Add(pDiceHaitiList[J][I]) == false) return false;
            }
        }
        return true;
    }

    struct JyoutaiDef2
    {
        internal int CurrP;
        internal int[] Curr6MenArr;
    }

    //30個のダイスを求める
    static List<int[]> Derive6MenArrList()
    {
        var WillReturn = new List<int[]>();

        var stk = new Stack<JyoutaiDef2>();
        JyoutaiDef2 WillPush;
        WillPush.CurrP = 5;
        WillPush.Curr6MenArr = new int[5 + 1];
        WillPush.Curr6MenArr[2] = 1; //底面は、固定で1とする
        stk.Push(WillPush);

        while (stk.Count > 0) {
            JyoutaiDef2 Popped = stk.Pop();

            //クリア判定
            if (Popped.CurrP == -1) {
                WillReturn.Add(Popped.Curr6MenArr.ToArray());
                continue;
            }

            //上面は、底面以外の5通り
            if (Popped.CurrP == 5) {
                for (int I = 2; I <= 6; I++) {
                    WillPush.CurrP = 0;
                    WillPush.Curr6MenArr = (int[])Popped.Curr6MenArr.Clone();
                    WillPush.Curr6MenArr[5] = I;
                    stk.Push(WillPush);
                }
            }
            //側面は、残りの4つの数での円順列となる
            else if (Popped.CurrP == 0) {
                //最初の側面は、未使用数の最小値とする
                for (int I = 2; I <= 6; I++) {
                    if (Array.IndexOf(Popped.Curr6MenArr, I) >= 0)
                        continue;
                    WillPush.CurrP = 1;
                    WillPush.Curr6MenArr = (int[])Popped.Curr6MenArr.Clone();
                    WillPush.Curr6MenArr[0] = I;
                    stk.Push(WillPush);
                    break;
                }
            }
            else {
                for (int I = 2; I <= 6; I++) {
                    if (Array.IndexOf(Popped.Curr6MenArr, I) >= 0)
                        continue;
                    if (Popped.CurrP == 1) WillPush.CurrP = 3;
                    if (Popped.CurrP == 3) WillPush.CurrP = 4;
                    if (Popped.CurrP == 4) WillPush.CurrP = -1;
                    WillPush.Curr6MenArr = (int[])Popped.Curr6MenArr.Clone();
                    WillPush.Curr6MenArr[Popped.CurrP] = I;
                    stk.Push(WillPush);
                }
            }
        }
        return WillReturn;
    }

    //1つのダイスの、使用する4面の候補を求める
    static List<int[]> DeriveUse4MenArrList(int[] p6MenArr)
    {
        var WillReturn = new List<int[]>();

        Action<int, int> wkAct = (pDelInd1, pDelInd2) =>
        {
            var wk4MenList = new List<int>(p6MenArr);

            //2と5以外の4面を使用する場合は、番号順にならないので入れ替え
            if (pDelInd1 == 2 && pDelInd2 == 5) {
                int wkChar = wk4MenList[3];
                wk4MenList[3] = wk4MenList[4];
                wk4MenList[4] = wkChar;
            }

            wk4MenList.RemoveAt(Math.Max(pDelInd1, pDelInd2));
            wk4MenList.RemoveAt(Math.Min(pDelInd1, pDelInd2));

            WillReturn.AddRange(DeriveUse4MenArr(wk4MenList.ToArray()));
        };

        wkAct(0, 4); //0と4以外の4面を使用
        wkAct(1, 3); //1と3以外の4面を使用
        wkAct(2, 5); //2と5以外の4面を使用
        return WillReturn;
    }

    //使用する4面の組み合わせを求める(8通り)
    static List<int[]> DeriveUse4MenArr(int[] p4MenArr)
    {
        var WillReturn = new List<int[]>();

        //正順の4つ
        for (int StaPos = 0; StaPos <= UB; StaPos++) {
            var WillAddList = new List<int>();
            for (int KasanP = 0; KasanP <= UB; KasanP++) {
                int TargetPos = StaPos + KasanP;
                if (TargetPos > UB) TargetPos -= (UB + 1);
                WillAddList.Add(p4MenArr[TargetPos]);
            }
            WillReturn.Add(WillAddList.ToArray());
        }

        //逆順の4つ
        for (int StaPos = 0; StaPos <= UB; StaPos++) {
            var WillAddList = new List<int>();
            for (int GenzanP = 0; GenzanP <= UB; GenzanP++) {
                int TargetPos = StaPos - GenzanP;
                if (TargetPos < 0) TargetPos += (UB + 1);
                WillAddList.Add(p4MenArr[TargetPos]);
            }
            WillReturn.Add(WillAddList.ToArray());
        }
        return WillReturn;
    }
}

実行結果

ダイス番号0の展開図は、251436
ダイス番号1の展開図は、251346
ダイス番号2の展開図は、241536
ダイス番号3の展開図は、241356
ダイス番号4の展開図は、231546
ダイス番号5の展開図は、231456
ダイス番号6の展開図は、261435
ダイス番号7の展開図は、261345
ダイス番号8の展開図は、241635
ダイス番号9の展開図は、241365
ダイス番号10の展開図は、231645
ダイス番号11の展開図は、231465
ダイス番号12の展開図は、261534
ダイス番号13の展開図は、261354
ダイス番号14の展開図は、251634
ダイス番号15の展開図は、251364
ダイス番号16の展開図は、231654
ダイス番号17の展開図は、231564
ダイス番号18の展開図は、261543
ダイス番号19の展開図は、261453
ダイス番号20の展開図は、251643
ダイス番号21の展開図は、251463
ダイス番号22の展開図は、241653
ダイス番号23の展開図は、241563
ダイス番号24の展開図は、361542
ダイス番号25の展開図は、361452
ダイス番号26の展開図は、351642
ダイス番号27の展開図は、351462
ダイス番号28の展開図は、341652
ダイス番号29の展開図は、341562
省略
3900000回目のPop内容=0,2,11,20,26。経過時間=00:25:16.8306642
4000000回目のPop内容=0,1,20,22,24。経過時間=00:25:54.1697671
4100000回目のPop内容=0,1,5,9,15,19。経過時間=00:26:35.8298607
解となるダイス番号リストは0,17,20,23,26,29で、3通り

解説

30個のダイスの中の任意の1つを必ず使うとし、
深さ優先探索で、全ての解を列挙してます。

23-01 時間どろぼう