Cマガ電脳クラブ(第094回) デジタル図形

問題

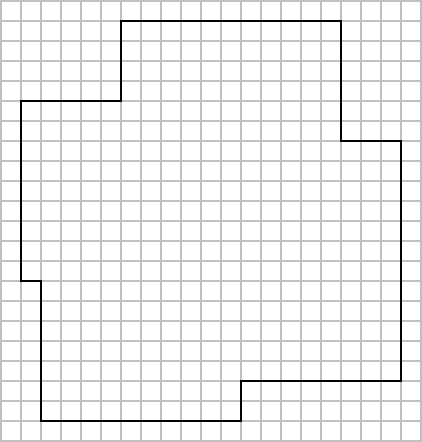
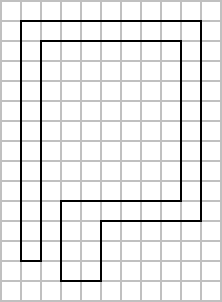
1〜12の長さの棒をすべて1本ずつ使って、平面の上に置いて図形を作る。
このとき、以下の条件を満たさなければならない。
　１) 棒と棒は端点のみで接し、ひとつの端点にはひとつの端点しか接しない
　２) 接した棒同士は必ず90度の角度を持つ
　３) 棒と棒は重ねたりクロスさせたりしない
　４) できた図形は閉じている (つまり12本が一続きとなる)
以上の条件を満たすようにして完成した図形の例がFig.1である。この図形の面積Sは158だが、
では、上記の条件で作れる図形の最大および最小の面積はいくつだろうか。
そのときの図形の例も添えてお願いする。

Fig.1 S=158の場合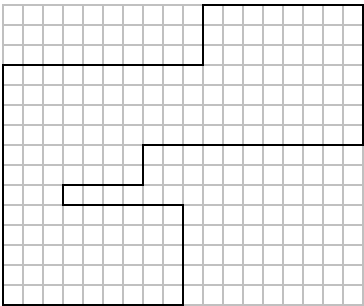

ソース

実行結果

解説

メモ 答えは
最小 41 ( 0, 0)-( 1, 0)-( 1,11)-( 8,11)-(8, 3)
       -( 2, 3)-( 2,-1)-( 4,-1)-( 4, 2)-(9, 2)
       -( 9,12)-( 0,12)-( 0, 0)


最大319 ( 0, 0)-( 1, 0)-( 1,-7)-(11,-7)-(11,-5)
       -(19,-5)-(19, 7)-(16, 7)-(16,13)-( 5,13)
       -( 5, 9)-( 0, 9)-( 0, 0)