Cマガ電脳クラブ(第108回) 最後の聖銭

問題

18枚の硬貨をFig.1のように円状に並べてＮ氏はいった。
「まず、好きな数をひとつだけいってくれ。正の整数だ。これを"聖数"としよう。
聖数が決まったら、この1円玉 (図中の矢印から) スタートして、時計回りに1、2、3・・・と順に硬貨を数えていく。
"聖数"まで数えたら、その場所にある硬貨を取り除く。
たとえば聖数が5なら、Aの10円玉が取り除かれる。

続いて、残りの硬貨をよせて再び円状にして、
その取り除いた場所の次のコインからまた時計回りに1、2、3・・・と聖数まで数え、その場所の硬貨を取り除く。
またその取り除いた場所の次の硬貨から・・・と、これを繰り返し、硬貨を取り除いていく。
そう、最後の2個になると、『ずいずいずっころばし状態』となるわけだ。
このようにして最後に1個残った硬貨を君にあげよう。」

さて、図中に1個だけある500円玉を手に入れるには、聖数として何といえばいいのだろうか。
答えはいくつもあるので、最小の数をお答えいただきたい。

Fig.1

ソース

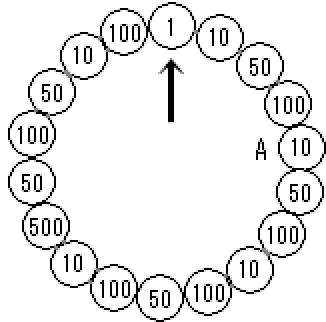
using System;
using System.Collections.Generic;

class Program
{
    static void Main()
    {
        for (int I = 1; I < int.MaxValue; I++) {
            if (IsAnswer(I)) {
                Console.WriteLine("解={0}", I);
                break;
            }
        }
    }

    //聖数を引数として、解かを判定
    static bool IsAnswer(int pSeisuu)
    {
        var NumList = new List<int>();
        NumList.AddRange(new int[] { 1, 10, 50, 100, 10, 50, 100, 10, 100, 50 });
        NumList.AddRange(new int[] { 100, 10, 500, 50, 100, 50, 10, 100 });
        int CurrInd = 0;

        while (NumList.Count > 1) {
            int CurrUB = NumList.Count - 1;
            CurrInd += pSeisuu - 1;
            if (CurrUB < CurrInd) CurrInd %= NumList.Count;
            if (NumList[CurrInd] == 500) return false;
            NumList.RemoveAt(CurrInd);
        }
        return true;
    }
}

実行結果

解=92

解説

Listクラスを使ってます。