Cマガ電脳クラブ(第128回) リング平方数

問題

Fig.1のように、1〜15の15個の数を環状に並べた。
すると、隣り合った2数の和がすべて平方数(ある数の2乗になっている数)になった・・・
と思ってよく見たら、1か所平方数になっていない (8＋9=17) 。

では、「1〜NのN個の数をすべて1個ずつ使って環状に並べ、隣り合う2数の和がすべて平方数になる」ものができるのは、
Nがいくつのときか。最小のNを求めよ。
また、そのNでの並べ方は、回転・鏡像解を除いて何通りあるか。

Fig.1 リング平方数

ソース

using System;
using System.Collections.Generic;
using System.Linq;

class Program
{
    static void Main()
    {
        for (int I = 2; I < int.MaxValue; I++) {
            Console.WriteLine("N={0}で解を調査中", I);
            if (ExecDFS(I)) break;
        }
    }

    struct JyoutaiDef
    {
        internal List<int> NumList;
    }

    //Nを引数として、深さ優先探索で解を探す
    static bool ExecDFS(int pN)
    {
        bool IsFound = false;

        var stk = new Stack<JyoutaiDef>();
        JyoutaiDef WillPush;
        WillPush.NumList = new List<int>() { 1 };
        stk.Push(WillPush);

        int AnswerCnt = 0;
        while (stk.Count > 0) {
            JyoutaiDef Popped = stk.Pop();

            //クリア判定
            if (Popped.NumList.Count == pN) {
                IsFound = true;
                var sb = new System.Text.StringBuilder();
                sb.AppendFormat("解{0}を発見", ++AnswerCnt);
                sb.AppendLine();
                for (int I = 0; I <= Popped.NumList.Count - 1; I++) {
                    if (I >= 10 && I % 10 == 0) sb.AppendLine();
                    else if (I > 0) sb.Append(',');
                    sb.AppendFormat("{0,2}", Popped.NumList[I]);
                }
                Console.WriteLine(sb.ToString());
                continue;
            }

            for (int I = 1; I <= pN; I++) {
                if (Popped.NumList.Contains(I)) continue;

                WillPush.NumList = new List<int>(Popped.NumList);
                WillPush.NumList.Add(I);

                //対称解の除外で、1の右隣 < 1の左隣
                if (pN >= 3 && WillPush.NumList.Count == pN) {
                    if (WillPush.NumList[1] > WillPush.NumList.Last())
                        continue;
                }

                //差が平方数であること
                Func<int, int, bool> wkFunc = (pInd1, pInd2) =>
                {
                    int wkSum = WillPush.NumList[pInd1] + WillPush.NumList[pInd2];
                    return IsHeihouSuu(wkSum);
                };

                int CurrInd = WillPush.NumList.Count - 1;
                if (wkFunc(CurrInd - 1, CurrInd) == false) continue;

                if (WillPush.NumList.Count == pN) {
                    if (wkFunc(0, CurrInd) == false) continue;
                }

                stk.Push(WillPush);
            }
        }
        return IsFound;
    }

    //平方数かを判定
    static bool IsHeihouSuu(int pVal)
    {
        for (int I = 0; I * I <= pVal; I++) {
            if (I * I == pVal) return true;
        }
        return false;
    }
}

実行結果

省略
N=30で解を調査中
N=31で解を調査中
N=32で解を調査中
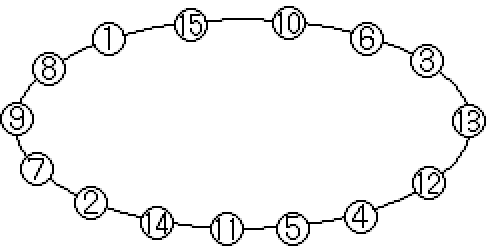
解1を発見
 1, 8,28,21, 4,32,17,19,30, 6
 3,13,12,24,25,11, 5,31,18, 7
29,20,16, 9,27,22,14, 2,23,26
10,15

解説

深さ優先探索でナイーブに解いてます。