Cマガ電脳クラブ(第138回) 運のいい分数

問題

「分母と分子にある同じ数字を消す」という間違った約分を、Fig.1の分数に対して行った。
すると運のいいことに、正しく約分した値と同じになったではないか。
この「運のいい分数」は無限にあるので、下のような条件をつける。
  1) 分母と分子で同じ数字があればそのペアは必ず消す
  2) 消されるペアは、分母と分子に1文字ずつしか入っていない。
      つまり、消すペアは一意に決まり、また、同じ数字で複数のペアが存在することもない
  3) 最終的に分母分子がそれぞれ1桁でできた、1未満の既約分数となる
  4) 数字の0 (ゼロ) は使わない
  5) 負の分数は考えない
この条件で、上記の間違った約分を行った結果が正しく約分した値と同じになる
「運のいい分数」は何通りあるだろうか。

Fig.1 分数
     

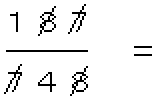
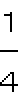
ソース

using System;
using System.Collections.Generic;
using System.Linq;

class Program
{
    static int mAnswerCnt = 0;

    static void Main()
    {
        var sw = System.Diagnostics.Stopwatch.StartNew();

        //基準となる既約分数を列挙
        for (int LoopBunbo = 2; LoopBunbo <= 9; LoopBunbo++) {
            for (int LoopBunsi = 1; LoopBunsi <= LoopBunbo - 1; LoopBunsi++) {
                if (DeriveGCD(LoopBunbo, LoopBunsi) != 1) continue;

                Console.WriteLine("基準となる既約分数{0}/{1}で、解を調査中。", LoopBunsi, LoopBunbo);
                DeriveAnswer(LoopBunbo, LoopBunsi);
            }
        }
        Console.WriteLine("解は{0}通り。経過時間={1}", mAnswerCnt, sw.Elapsed);
    }

    //ユークリッドの互除法で2数の最大公約数を求める
    static private int DeriveGCD(int pVal1, int pVal2)
    {
        pVal1 = Math.Abs(pVal1);
        pVal2 = Math.Abs(pVal2);

        int WarareruKazu = Math.Max(pVal1, pVal2);
        int WaruKazu = Math.Min(pVal1, pVal2);

        while (true) {
            int Amari = WarareruKazu % WaruKazu;
            if (Amari == 0) return WaruKazu;
            WarareruKazu = WaruKazu;
            WaruKazu = Amari;
        }
    }

    //既約分数の分母と分子を引数とし、解を列挙
    static void DeriveAnswer(int pBunbo, int pBunsi)
    {
        int wkBunbo = pBunbo;
        int wkBunsi = pBunsi;

        while (true) {
            wkBunbo += pBunbo;
            wkBunsi += pBunsi;

            //分母が9桁だと、分子が消えてしまうので
            //分母が8桁の最大値を超えたらBreak
            if (wkBunbo > 98765432) break;

            //10の倍数なら不適
            if (wkBunbo % 10 == 0) continue;
            if (wkBunsi % 10 == 0) continue;

            List<int> BunboNumList = DeriveNumList(wkBunbo);
            if (BunboNumList.Contains(0)) continue;
            if (BunboNumList.Count > BunboNumList.Distinct().Count()) continue;

            List<int> BunsiNumList = DeriveNumList(wkBunsi);
            if (BunsiNumList.Contains(0)) continue;
            if (BunsiNumList.Count > BunsiNumList.Distinct().Count()) continue;

            //桁数が違うと不適
            if (BunboNumList.Count > BunsiNumList.Count) continue;

            for (int J = 1; J <= 9; J++) {
                if (BunboNumList.Contains(J) == false) continue;
                if (BunsiNumList.Contains(J) == false) continue;
                BunboNumList.Remove(J);
                BunsiNumList.Remove(J);
            }

            //間違った約分後の、分母と分子が一致すること
            if (BunboNumList.Count != 1) continue;
            if (BunsiNumList.Count != 1) continue;
            if (pBunbo != BunboNumList[0]) continue;
            if (pBunsi != BunsiNumList[0]) continue;

            mAnswerCnt++;
            Console.WriteLine("解{0}を発見。{1}/{2}", mAnswerCnt, wkBunsi, wkBunbo);
        }
    }

    //数値から数字のListを求めて返す
    static List<int> DeriveNumList(int pVal)
    {
        var WillReturn = new List<int>();
        int CopiedVal = pVal;
        do {
            int ModVal = CopiedVal % 10;
            WillReturn.Add(ModVal);
            CopiedVal /= 10;
        } while (CopiedVal > 0);
        return WillReturn;
    }
}

実行結果

省略
基準となる既約分数8/9で、解を調査中。
解305を発見。23768/26739
解306を発見。82376/92673
解307を発見。317528/357219
解308を発見。486152/546921
解309を発見。615248/692154
解310を発見。831752/935721
解311を発見。2457368/2764539
解312を発見。2485736/2796453
解313を発見。3846752/4327596
解314を発見。3875264/4359672
解315を発見。4235768/4765239
解316を発見。5736248/6453279
解317を発見。5736824/6453927
解318を発見。6438752/7243596
解319を発見。6752384/7596432
解320を発見。8245736/9276453
解321を発見。8423576/9476523
解322を発見。8573624/9645327
解は322通り。経過時間=00:06:45.5474491

解説

分子と分母が1桁な既約分数から、解を列挙してます。