Cマガ電脳クラブ(第141回) くろ交換しろ

問題

Fig.1のようなマスが描かれた盤があり、そのマスに白・黒のコマそれぞれ3個が置かれている。
このFig.1の状態からコマを順次動かして、白と黒のコマの場所を入れ替えたい (Fig.2の状態にしたい) 。

コマを移動する際の条件は以下のとおり。
　1) コマは常にマス内に存在し、各マスには1つしかコマは入れない
　2) あるコマの隣のマスが空いていれば移動できる。隣とは上下左右のマスを指し、斜めは考えない
　3) コマがほかのマスに移動するとそれを1手と数える。
　   ただし、同じコマが連続して移動する場合は、止まるまでをまとめて1手とする

この条件で、最低何手で完成できるだろうか。「盤全体を180度回転する」なんていうのは、ここでは考えない。

     

ソース

using System;
using System.Collections.Generic;

class Program
{
    const int UB_X = 4 - 1;
    const int UB_Y = 7 - 1;

    struct JyoutaiDef
    {
        internal char[,] BanArr;
        internal int Level;
        internal List<string> Log;
    }

    static void Main()
    {
        var Que = new Queue<JyoutaiDef>();
        JyoutaiDef WillEnqueue;
        WillEnqueue.BanArr = new char[UB_X + 1, UB_Y + 1];

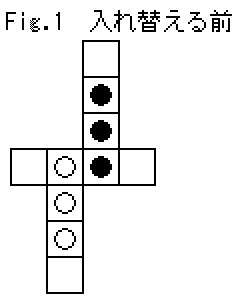
        string[] wkStrArr ={"** *",
                            "**B*",
                            "**B*",
                            " WB ",
                            "*W**",
                            "*W**",
                            "* **"};
        for (int Y = 0; Y <= wkStrArr.GetUpperBound(0); Y++) {
            for (int X = 0; X <= wkStrArr[Y].Length - 1; X++) {
                WillEnqueue.BanArr[X, Y] = wkStrArr[Y][X];
            }
        }

        WillEnqueue.Level = 0;
        WillEnqueue.Log = new List<string>();
        WillEnqueue.Log.Add(BanToStr(WillEnqueue.BanArr));
        Que.Enqueue(WillEnqueue);

        var VisitedSet = new HashSet<int>();
        VisitedSet.Add(GetHash(WillEnqueue.BanArr));

        while (Que.Count > 0) {
            JyoutaiDef Dequeued = Que.Dequeue();

            //クリア判定
            if (IsClear(Dequeued.BanArr)) {
                Console.WriteLine("{0}手の解を発見", Dequeued.Level);

                for (int I = 0; I <= Dequeued.Log.Count - 1; I++) {
                    Console.WriteLine("{0}手目", I);
                    Console.WriteLine(Dequeued.Log[I]);
                }
                return;
            }

            for (int X = 0; X <= UB_X; X++) {
                for (int Y = 0; Y <= UB_Y; Y++) {
                    if (Dequeued.BanArr[X, Y] != 'B' && Dequeued.BanArr[X, Y] != 'W')
                        continue;

                    foreach (PointDef EachToPos in DeriveToPosArr(Dequeued.BanArr, X, Y)) {
                        WillEnqueue.BanArr = (char[,])Dequeued.BanArr.Clone();
                        WillEnqueue.BanArr[EachToPos.X, EachToPos.Y] = WillEnqueue.BanArr[X, Y];
                        WillEnqueue.BanArr[X, Y] = ' ';

                        //訪問済ノードなら枝切り
                        if (VisitedSet.Add(GetHash(WillEnqueue.BanArr)) == false)
                            continue;

                        WillEnqueue.Level = Dequeued.Level + 1;
                        WillEnqueue.Log = new List<string>(Dequeued.Log);
                        WillEnqueue.Log.Add(BanToStr(WillEnqueue.BanArr));
                        Que.Enqueue(WillEnqueue);
                    }
                }
            }
        }
    }

    //クリア判定
    static bool IsClear(char[,] pBanArr)
    {
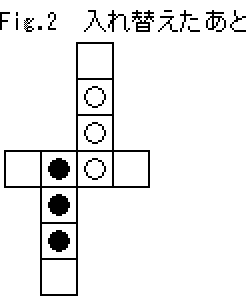
        for (int LoopY = 1; LoopY <= 3; LoopY++)
            if (pBanArr[2, LoopY] != 'W') return false;

        for (int LoopY = 3; LoopY <= 5; LoopY++)
            if (pBanArr[1, LoopY] != 'B') return false;

        return true;
    }

    struct PointDef
    {
        internal int X;
        internal int Y;
    }

    //移動元のコマの座標を引数として、移動先の座標の配列を返す
    static PointDef[] DeriveToPosArr(char[,] pBanArr, int pFromX, int pFromY)
    {
        var ToPosList = new List<PointDef>();

        var stk = new Stack<PointDef>();
        PointDef WillPush;
        WillPush.X = pFromX;
        WillPush.Y = pFromY;
        stk.Push(WillPush);

        while (stk.Count > 0) {
            PointDef Popped = stk.Pop();

            Action<int, int> PushSyori = (pNewX, pNewY) =>
            {
                if (pNewX < 0 || UB_X < pNewX) return;
                if (pNewY < 0 || UB_Y < pNewY) return;

                if (pBanArr[pNewX, pNewY] != ' ') return;

                //再訪不可
                if (pNewX == pFromX && pNewY == pFromY) return;
                if (ToPosList.Exists(A => A.X == pNewX && A.Y == pNewY)) return;

                PointDef wkPoint = new PointDef() { X = pNewX, Y = pNewY };
                ToPosList.Add(wkPoint);
                stk.Push(wkPoint);
            };

            PushSyori(Popped.X, Popped.Y - 1);
            PushSyori(Popped.X, Popped.Y + 1);
            PushSyori(Popped.X - 1, Popped.Y);
            PushSyori(Popped.X + 1, Popped.Y);
        }
        return ToPosList.ToArray();
    }

    //盤面をハッシュ値に変換
    static int GetHash(char[,] pBanArr)
    {
        var NumList = new List<int>();

        for (int X = 0; X <= UB_X; X++) {
            for (int Y = 0; Y <= UB_Y; Y++) {
                if (pBanArr[X, Y] == '*') continue;
                if (pBanArr[X, Y] == ' ') NumList.Add(0);
                if (pBanArr[X, Y] == 'B') NumList.Add(1);
                if (pBanArr[X, Y] == 'W') NumList.Add(2);
            }
        }
        //3の10乗=59049なので3進数ならオーバーフローしない
        int WillReturn = 0;
        foreach (int EachInt in NumList) {
            WillReturn *= 3;
            WillReturn += EachInt;
        }
        return WillReturn;
    }

    //盤面をString型に変換
    static string BanToStr(char[,] pBanArr)
    {
        var sb = new System.Text.StringBuilder();
        for (int Y = 0; Y <= UB_Y; Y++) {
            for (int X = 0; X <= UB_X; X++) {
                sb.Append(pBanArr[X, Y]);
            }
            sb.AppendLine();
        }
        return sb.ToString();
    }
}

実行結果

22手の解を発見
0手目
** *
**B*
**B*
 WB
*W**
*W**
* **

1手目
** *
**B*
**B*
W B
*W**
*W**
* **

省略

解説

同一ノードへの再訪を防止した、幅優先探索で解いてます。