Cマガ電脳クラブ(第146回) 逆さ電卓数字

問題

デジタル時計や電卓に昔からよく使われている数字 (ここでは電卓数字と呼ぶ) の表記では、
逆さから見ても数字として読めるものがある。
つまり、0、1、2、5、6、8、9は、
逆さから0、1、2、5、9、8、6と読めるのだ。

さて、Fig.1の四角に逆さから読める電卓数字を1字ずつ入れて式を成り立たせ、
さらに全体を180度回転して逆さから見ても数式として成立するようにしたい。

Fig.1にその例を示す。このような式は例も入れて何通り作れるだろうか？
ただし、逆さにした場合も含めて各3桁の数の左端には0はこないこととし、
また、和をとっている2数を入れ替えたものは別の解とはしない。

Fig.1 逆さから見ても成立する式

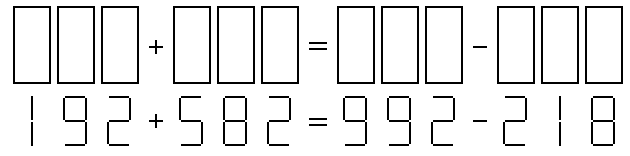
ソース

using System;
using System.Collections.Generic;

class Program
{
    static void Main()
    {
        //3桁の数の変換表を作成
        DeriveConvInfoArr();

        int AnswerCnt = 0;
        int wkUB = ConvInfoArr.GetUpperBound(0);
        foreach (ConvInfoDef ConvInfoA in ConvInfoArr) {
            if (ConvInfoA.BeforeVal > 900) break;
            if (ConvInfoA.AfterVal > 900) continue;
            foreach (ConvInfoDef ConvInfoB in ConvInfoArr) {
                if (ConvInfoA.BeforeVal > ConvInfoB.BeforeVal) continue;

                if (ConvInfoA.BeforeVal + ConvInfoB.BeforeVal > 900) break;
                if (ConvInfoA.AfterVal + ConvInfoB.AfterVal > 900) continue;
                foreach (ConvInfoDef ConvInfoC in ConvInfoArr) {
                    if (ConvInfoC.BeforeVal < 200) continue;
                    if (ConvInfoC.AfterVal > 900) continue;
                    foreach (ConvInfoDef ConvInfoD in ConvInfoArr) {
                        if (ConvInfoD.BeforeVal > 900) break;

                        int Sahen1 = ConvInfoA.BeforeVal + ConvInfoB.BeforeVal;
                        int Uhen1 = ConvInfoC.BeforeVal - ConvInfoD.BeforeVal;
                        if (Sahen1 != Uhen1) continue;

                        int Sahen2 = ConvInfoD.AfterVal - ConvInfoC.AfterVal;
                        int Uhen2 = ConvInfoB.AfterVal + ConvInfoA.AfterVal;
                        if (Sahen2 != Uhen2) continue;

                        Console.WriteLine("解{0}を発見。{1}+{2}={3}-{4}",
                            ++AnswerCnt, ConvInfoA.BeforeVal, ConvInfoB.BeforeVal,
                            ConvInfoC.BeforeVal, ConvInfoD.BeforeVal);
                    }
                }
            }
        }
    }

    struct ConvInfoDef
    {
        internal int BeforeVal;
        internal int AfterVal;
    }
    static ConvInfoDef[] ConvInfoArr;

    //3桁の数の変換表を作成
    static void DeriveConvInfoArr()
    {
        var ConvInfoList = new List<ConvInfoDef>();

        int[] BaseNum = { 0, 1, 2, 5, 6, 8, 9 };
        int wkUB = BaseNum.GetUpperBound(0);

        for (int I = 0; I <= wkUB; I++) {
            //100の位の0は不適
            if (BaseNum[I] == 0) continue;
            for (int J = 0; J <= wkUB; J++) {
                for (int K = 0; K <= wkUB; K++) {
                    //1の位の0は不適
                    if (BaseNum[K] == 0) continue;

                    int wkBeforeVal = BaseNum[K];
                    wkBeforeVal += 10 * BaseNum[J];
                    wkBeforeVal += 100 * BaseNum[I];

                    Func<int, int> wkFunc = pInt =>
                    {
                        if (pInt == 6) return 9;
                        if (pInt == 9) return 6;
                        return pInt;
                    };
                    int wkAfterVal = wkFunc(BaseNum[I]);
                    wkAfterVal += 10 * wkFunc(BaseNum[J]);
                    wkAfterVal += 100 * wkFunc(BaseNum[K]);

                    ConvInfoList.Add(
                        new ConvInfoDef() { BeforeVal = wkBeforeVal, AfterVal = wkAfterVal });
                }
            }
        }
        ConvInfoArr = ConvInfoList.ToArray();
    }
}

実行結果

省略
解190を発見。255+261=812-296
解191を発見。261+282=812-269
解192を発見。261+285=812-266
解193を発見。262+281=812-269
解194を発見。265+281=812-266
解195を発見。282+282=862-298

解説

3桁の数を、180度回転した後の変換表を、事前に作成してから、

A+B = C-D
RevD-RevC = RevB+RevA
となる組み合わせを列挙してます。