24-04 カックロ

問題

ニコリのカックロを解きます。

例題と答え
    

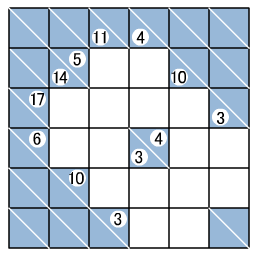
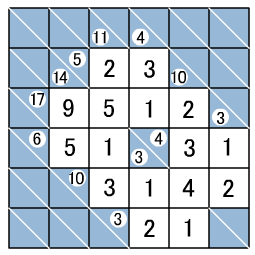1 すべての白マスに１から９までの数字のどれかを１つずつ入れましょう。０(ゼロ)は使いません。

2 ナナメの線の右上の数字は、その右に連続した白マスに入る数字の合計を表し、
  左下の数字は、その下に連続した白マスに入る数字の合計を表します。

3 タテヨコへの１つの白マスのつながりには、同じ数字を入れてはいけません。
  １２４は○ですが、２３２は×です。

ソース

using System;
using System.Collections.Generic;
using System.Linq;

class Program
{
    struct PointDef
    {
        internal int X;
        internal int Y;
    }

    //数値情報の構造体
    struct NumInfoDef
    {
        internal PointDef Point; //数値の座標
        internal int YokoSum; //横方向の合計
        internal int TateSum; //縦方向の合計
        internal PointDef[] RenketuYokoPointArr; //連結した横座標の配列
        internal PointDef[] RenketuTatePointArr; //連結した縦座標の配列
    }

    //カックロ分解表の1要素の定義
    struct BunkaiDef
    {
        internal int MasuCnt; //マス目の数
        internal int SumVal; //合計値
        internal int[] KouhoArr; //候補の数値の配列
    }

    //カックロ分解表
    static BunkaiDef[] mBunkaiArr;

    static int[,] mQuestionYokoSum;
    static int[,] mQuestionTateSum;
    static int UB_X;
    static int UB_Y;

    static NumInfoDef[] mNumInfoArr; //数値情報の配列

    static void Main()
    {
        //カックロ分解表を作成
        CreateBunkaiHyou();

        int[,] Q01_YokoSum = {{ 0, 5, 5, 0, 0},
                              {17,17,17,17, 0},
                              { 6, 6, 0, 4, 4},
                              { 0,10,10,10,10},
                              { 0, 0, 3, 3, 0}};

        int[,] Q01_TateSum = {{ 0,11, 4, 0, 0},
                              {14,11, 4,10, 0},
                              {14,11, 0,10, 3},
                              { 0,11, 3,10, 3},
                              { 0, 0, 3,10, 0}};

        mQuestionYokoSum = XYRev(Q01_YokoSum);
        mQuestionTateSum = XYRev(Q01_TateSum);
        UB_X = mQuestionYokoSum.GetUpperBound(0);
        UB_Y = mQuestionYokoSum.GetUpperBound(1);

        //第1フェーズ 数値情報を作成する
        CreateNumInfoArr();

        //デバッグ用の数値情報を出力
        //DebugPrintNumInfo();

        //第2フェーズ 確定探索
        int[,] FillNumArr = new int[UB_X + 1, UB_Y + 1];
        ExecKakuteiTansaku(FillNumArr);

        //第3フェーズ 深さ優先探索
        ExecDFS(FillNumArr);
    }

    //カックロ分解表を作成
    static void CreateBunkaiHyou()
    {
        var BunkaiList = new List<BunkaiDef>();

        Action<int, int, int[]> AddAct = (pMasuCnt, pSumVal, pKouhoArr) =>
        {
            BunkaiDef WillAdd;
            WillAdd.MasuCnt = pMasuCnt;
            WillAdd.SumVal = pSumVal;
            WillAdd.KouhoArr = pKouhoArr;
            BunkaiList.Add(WillAdd);
        };

        AddAct(2, 3, new int[] { 1, 2 });
        AddAct(2, 4, new int[] { 1, 3 });
        AddAct(2, 16, new int[] { 7, 9 });
        AddAct(2, 17, new int[] { 8, 9 });
        AddAct(3, 6, new int[] { 1, 2, 3 });
        AddAct(3, 7, new int[] { 1, 2, 4 });
        AddAct(3, 23, new int[] { 6, 8, 9 });
        AddAct(3, 24, new int[] { 7, 8, 9 });
        AddAct(4, 10, new int[] { 1, 2, 3, 4 });
        AddAct(4, 11, new int[] { 1, 2, 3, 5 });
        AddAct(4, 29, new int[] { 5, 7, 8, 9 });
        AddAct(4, 30, new int[] { 6, 7, 8, 9 });
        AddAct(5, 15, new int[] { 1, 2, 3, 4, 5 });
        AddAct(5, 16, new int[] { 1, 2, 3, 4, 6 });
        AddAct(5, 34, new int[] { 4, 6, 7, 8, 9 });
        AddAct(5, 35, new int[] { 5, 6, 7, 8, 9 });
        AddAct(6, 21, new int[] { 1, 2, 3, 4, 5, 6 });
        AddAct(6, 22, new int[] { 1, 2, 3, 4, 5, 7 });
        AddAct(6, 38, new int[] { 3, 5, 6, 7, 8, 9 });
        AddAct(6, 39, new int[] { 4, 5, 6, 7, 8, 9 });
        AddAct(7, 28, new int[] { 1, 2, 3, 4, 5, 6, 7 });
        AddAct(7, 29, new int[] { 1, 2, 3, 4, 5, 6, 8 });
        AddAct(7, 41, new int[] { 2, 4, 5, 6, 7, 8, 9 });
        AddAct(7, 42, new int[] { 3, 4, 5, 6, 7, 8, 9 });

        for (int I = 1; I <= 9; I++) {
            var wkList = Enumerable.Range(1, 9).ToList();
            wkList.Remove(I);
            AddAct(8, 45 - I, wkList.ToArray());
        }

        AddAct(9, 45, Enumerable.Range(1, 9).ToArray());

        mBunkaiArr = BunkaiList.ToArray();
    }

    //X座標とY座標の入れ替え
    static int[,] XYRev(int[,] pBaseArr)
    {
        int RevArrUB_X = pBaseArr.GetUpperBound(1);
        int RevArrUB_Y = pBaseArr.GetUpperBound(0);
        int[,] WillReturnArr = new int[RevArrUB_X + 1, RevArrUB_Y + 1];
        for (int X = 0; X <= RevArrUB_X; X++) {
            for (int Y = 0; Y <= RevArrUB_Y; Y++) {
                WillReturnArr[X, Y] = pBaseArr[Y, X];
            }
        }
        return WillReturnArr;
    }

    //第1フェーズ 数値情報を作成する
    static void CreateNumInfoArr()
    {
        var NumInfoList = new List<NumInfoDef>();

        for (int LoopX = 0; LoopX <= UB_X; LoopX++) {
            for (int LoopY = 0; LoopY <= UB_Y; LoopY++) {
                //黒マスの場合
                if (mQuestionYokoSum[LoopX, LoopY] == 0)
                    continue;

                NumInfoDef WillAdd;
                PointDef CurrPoint = new PointDef() { X = LoopX, Y = LoopY };
                WillAdd.Point = CurrPoint;
                WillAdd.YokoSum = mQuestionYokoSum[LoopX, LoopY];
                WillAdd.TateSum = mQuestionTateSum[LoopX, LoopY];

                var wkYokoPointList = new List<PointDef>();
                wkYokoPointList.AddRange(DeriveRenketuPointList(CurrPoint, -1, 0));
                wkYokoPointList.AddRange(DeriveRenketuPointList(CurrPoint, 1, 0));
                WillAdd.RenketuYokoPointArr =
                    wkYokoPointList.OrderBy(A => A.X).ThenBy(A => A.Y).ToArray();

                var wkTatePointList = new List<PointDef>();
                wkTatePointList.AddRange(DeriveRenketuPointList(CurrPoint, 0, -1));
                wkTatePointList.AddRange(DeriveRenketuPointList(CurrPoint, 0, 1));
                WillAdd.RenketuTatePointArr =
                    wkTatePointList.OrderBy(A => A.X).ThenBy(A => A.Y).ToArray();

                NumInfoList.Add(WillAdd);
            }
        }
        mNumInfoArr = NumInfoList.ToArray();
    }

    //変位ベクトルを引数として、連結した座標のListを返す
    static List<PointDef> DeriveRenketuPointList(PointDef pCurrPoint, int pHeniX, int pHeniY)
    {
        var WillReturnList = new List<PointDef>();

        int LoopX = pCurrPoint.X, LoopY = pCurrPoint.Y;

        while (true) {
            //次のマスからが対象となる
            LoopX += pHeniX; LoopY += pHeniY;

            //範囲外の場合
            if (LoopX < 0 || UB_X < LoopX) break;
            if (LoopY < 0 || UB_Y < LoopY) break;

            //黒マスに到達した場合
            if (mQuestionYokoSum[LoopX, LoopY] == 0) break;

            WillReturnList.Add(new PointDef() { X = LoopX, Y = LoopY });
        }
        return WillReturnList;
    }

    //デバッグ用の数値情報を出力
    static void DebugPrintNumInfo()
    {
        for (int I = 0; I <= mNumInfoArr.GetUpperBound(0); I++) {
            Console.WriteLine("■■■■■■■■■■■■■");
            Console.WriteLine("{0}個目の数値情報", I + 1);
            Console.WriteLine("Point=({0},{1})", mNumInfoArr[I].Point.X, mNumInfoArr[I].Point.Y);
            Console.WriteLine("横方向の合計={0}", mNumInfoArr[I].YokoSum);
            Console.WriteLine("縦方向の合計={0}", mNumInfoArr[I].TateSum);

            Console.Write("連結した横座標の配列 ");
            foreach (var EachPoint in mNumInfoArr[I].RenketuYokoPointArr) {
                Console.Write("({0},{1}),", EachPoint.X, EachPoint.Y);
            }

            Console.WriteLine();
            Console.Write("連結した縦座標の配列 ");
            foreach (var EachPoint in mNumInfoArr[I].RenketuTatePointArr) {
                Console.Write("({0},{1}),", EachPoint.X, EachPoint.Y);
            }
            Console.WriteLine();
        }
    }

    //第2フェーズ 確定探索を行い、有効な盤面かを返す
    static bool ExecKakuteiTansaku(int[,] pFillNumArr)
    {
        while (true) {
            int[,] PrevNumArr = (int[,])pFillNumArr.Clone();

            for (int I = 0; I <= mNumInfoArr.GetUpperBound(0); I++) {
                int CurrX = mNumInfoArr[I].Point.X;
                int CurrY = mNumInfoArr[I].Point.Y;
                if (pFillNumArr[CurrX, CurrY] != 0) continue;

                //状態を調査して、数値の候補を求める
                int[] KouhoNumArr = DeriveKouhoNumArr(pFillNumArr, I, CurrX, CurrY);

                if (KouhoNumArr.Length == 0) {
                    return false;
                }
                else if (KouhoNumArr.Length == 1) {
                    pFillNumArr[CurrX, CurrY] = KouhoNumArr[0];
                }
            }

            //確定探索で確定するマスがなくなったらBreak
            if (pFillNumArr.Cast<int>().SequenceEqual(PrevNumArr.Cast<int>()))
                break;
        }
        return true;
    }

    //状態を調査して、数値の候補を求める
    static int[] DeriveKouhoNumArr(int[,] pFillNumArr, int pInd, int pX, int pY)
    {
        //横方向の合計値を求める
        int Sum_Yoko = mNumInfoArr[pInd].YokoSum;

        //縦方向の合計値を求める
        int Sum_Tate = mNumInfoArr[pInd].TateSum;

        //横方向の使用済の数値を求める
        var UsedNumSet_Yoko = new HashSet<int>();
        foreach (PointDef EachPoint in mNumInfoArr[pInd].RenketuYokoPointArr) {
            int wkVal = pFillNumArr[EachPoint.X, EachPoint.Y];
            if (wkVal != 0) UsedNumSet_Yoko.Add(wkVal);
        }

        //縦方向の使用済の数値を求める
        var UsedNumSet_Tate = new HashSet<int>();
        foreach (PointDef EachPoint in mNumInfoArr[pInd].RenketuTatePointArr) {
            int wkVal = pFillNumArr[EachPoint.X, EachPoint.Y];
            if (wkVal != 0) UsedNumSet_Tate.Add(wkVal);
        }

        //横方向の残マスを求める
        int RestMasuCnt_Yoko = 1;
        RestMasuCnt_Yoko += mNumInfoArr[pInd].RenketuYokoPointArr.Length;
        RestMasuCnt_Yoko -= UsedNumSet_Yoko.Count;

        //縦方向の残マスを求める
        int RestMasuCnt_Tate = 1;
        RestMasuCnt_Tate += mNumInfoArr[pInd].RenketuTatePointArr.Length;
        RestMasuCnt_Tate -= UsedNumSet_Tate.Count;

        HashSet<int> wk1 = DeriveKouhoNumSet_OneLine(Sum_Yoko, UsedNumSet_Yoko, RestMasuCnt_Yoko);
        HashSet<int> wk2 = DeriveKouhoNumSet_OneLine(Sum_Tate, UsedNumSet_Tate, RestMasuCnt_Tate);
        return wk1.Intersect(wk2).ToArray();
    }

    //横方向か縦方向の数値の候補を求める
    static HashSet<int> DeriveKouhoNumSet_OneLine(int pLineSum, HashSet<int> pUsedNumSet, int pRestMasuCnt)
    {
        var KouhoSet = new HashSet<int>();
        int pRestSum = pLineSum - pUsedNumSet.Sum();

        //対応するカックロ分解表があるかを調べる
        int TaiouInd = Array.FindIndex(mBunkaiArr, X => X.SumVal == pRestSum && X.MasuCnt == pRestMasuCnt);

        if (TaiouInd >= 0) { //対応するカックロ分解表がある場合
            KouhoSet.UnionWith(mBunkaiArr[TaiouInd].KouhoArr);
        }
        //残りマスが1マスの場合
        else if (pRestMasuCnt == 1) {
            if (pRestSum <= 9) KouhoSet.Add(pRestSum);
        }
        else { //対応するカックロ分解表がない場合
            for (int I = 1; I <= 9; I++) {
                //残りマス数-1を項数とする
                int Kousuu = pRestMasuCnt - 1;

                var MinOtherNumList = new List<int>();
                var MaxOtherNumList = new List<int>();

                for (int J = 1; J <= 9; J++) {
                    if (J == I || pUsedNumSet.Contains(J)) continue;
                    MinOtherNumList.Add(J);
                    if (MinOtherNumList.Count == Kousuu) break;
                }
                for (int J = 9; 0 <= J; J--) {
                    if (J == I || pUsedNumSet.Contains(J)) continue;
                    MaxOtherNumList.Add(J);
                    if (MaxOtherNumList.Count == Kousuu) break;
                }

                if (pRestSum < I + MinOtherNumList.Sum()) continue;
                if (pRestSum > I + MaxOtherNumList.Sum()) continue;
                KouhoSet.Add(I);
            }

            //残りマスが2マスで、合計が偶数なら、2で割った値は使用不可
            if (pRestMasuCnt == 2 && pRestSum % 2 == 0)
                KouhoSet.Remove(pRestSum / 2);
        }

        //使用済の数値は使用不可
        KouhoSet.ExceptWith(pUsedNumSet);

        return KouhoSet;
    }

    //第3フェーズ 深さ優先探索
    static void ExecDFS(int[,] pFillNumArr)
    {
        var Stk = new Stack<int[,]>();
        int[,] WillPushFillNumArr = pFillNumArr;
        Stk.Push(WillPushFillNumArr);

        while (Stk.Count > 0) {
            int[,] PoppedFillNumArr = Stk.Pop();

            //クリア判定
            int Ind;
            int NeedFillX, NeedFillY;
            if (IsClear(PoppedFillNumArr, out Ind, out NeedFillX, out NeedFillY)) {
                Console.WriteLine("解を発見");
                PrintAnswer(PoppedFillNumArr);
                return;
            }

            //状態を調査して、数値の候補を求める
            int[] KouhoNumArr = DeriveKouhoNumArr(PoppedFillNumArr, Ind, NeedFillX, NeedFillY);

            //Push処理
            foreach (int EachInt in KouhoNumArr) {
                WillPushFillNumArr = (int[,])PoppedFillNumArr.Clone();
                WillPushFillNumArr[NeedFillX, NeedFillY] = EachInt;

                //確定探索を行い、有効な盤面ならPush処理
                if (ExecKakuteiTansaku(WillPushFillNumArr))
                    Stk.Push(WillPushFillNumArr);
            }
        }
    }

    //クリア判定
    static bool IsClear(int[,] pFillNumArr, out int pInd, out int pNeedFillX, out int pNeedFillY)
    {
        pInd = -1;
        pNeedFillX = pNeedFillY = -1;
        for (int LoopX = 0; LoopX <= UB_X; LoopX++) {
            for (int LoopY = 0; LoopY <= UB_Y; LoopY++) {
                if (pFillNumArr[LoopX, LoopY] != 0) continue;

                int wkInd = Array.FindIndex(mNumInfoArr,
                    A => A.Point.X == LoopX && A.Point.Y == LoopY);

                if (wkInd >= 0) {
                    pInd = wkInd; pNeedFillX = LoopX; pNeedFillY = LoopY;
                    return false;
                }
            }
        }
        return true;
    }

    //解を出力
    static void PrintAnswer(int[,] pFillNumArr)
    {
        //半角数字を全角数字に変換
        Func<int, char> SingleToWideFunc = (pStr) => (char)('０' + pStr);

        var sb = new System.Text.StringBuilder();
        for (int LoopY = 0; LoopY <= UB_Y; LoopY++) {
            for (int LoopX = 0; LoopX <= UB_X; LoopX++) {
                int wkInt = pFillNumArr[LoopX, LoopY];
                if (wkInt != 0) {
                    sb.Append(SingleToWideFunc(wkInt));
                }
                else if (Array.Exists(mNumInfoArr,
                         A => A.Point.X == LoopX && A.Point.Y == LoopY)) {
                    sb.Append('□');
                }
                else sb.Append('■');
            }
            sb.AppendLine();
        }
        Console.WriteLine(sb.ToString());
    }
}

実行結果

解を発見
■２３■■
９５１２■
５１■３１
■３１４２
■■２１■

追加問題02 ニコリビヨリのサンプル問題

int[,] Q02_YokoSum = {{ 0, 3, 3, 0, 0},
                      {16,16,16,16,16},
                      {11,11, 0, 9, 9},
                      {35,35,35,35,35},
                      { 0, 0,17,17, 0}};

int[,] Q02_TateSum = {{ 0,11, 4, 0, 0},
                      {16,11, 4,30,14},
                      {16,11, 0,30,14},
                      {16,11,16,30,14},
                      { 0, 0,16,30, 0}};

追加問題03 ニコリビヨリの問題

int[,] Q03_YokoSum = {{ 4, 4, 0, 3, 3, 0, 0, 0,18,18,18},
                      { 3, 3, 0, 6, 6, 6, 0,10,10,10,10},
                      {10,10,10,10, 0,11,11,11,11, 0, 0},
                      { 0, 7, 7, 0, 7, 7, 7, 0,11,11,11},
                      { 0, 0, 8, 8, 8, 0, 7, 7, 0,16,16},
                      { 0, 9, 9, 9, 0, 0, 0,21,21,21, 0},
                      { 6, 6, 0,10,10, 0,22,22,22, 0, 0},
                      { 6, 6, 6, 0,23,23,23, 0,17,17, 0},
                      { 0, 0,29,29,29,29, 0,26,26,26,26},
                      {15,15,15,15, 0,24,24,24, 0, 6, 6},
                      { 7, 7, 7, 0, 0, 0,16,16, 0,12,12}};

int[,] Q03_TateSum = {{ 7,10, 0, 6, 4, 0, 0, 0,11,10,13},
                      { 7,10, 0, 6, 4, 7, 0, 3,11,10,13},
                      { 7,10,11, 6, 0, 7, 6, 3,11, 0, 0},
                      { 0,10,11, 0, 3, 7, 6, 0,11,23, 8},
                      { 0, 0,11, 7, 3, 0, 6,23, 0,23, 8},
                      { 0, 9,11, 7, 0, 0, 0,23,30,23, 0},
                      { 4, 9, 0, 7,24, 0,13,23,30, 0, 0},
                      { 4, 9,11, 0,24,24,13, 0,30,29, 0},
                      { 0, 0,11,10,24,24, 0,24,30,29, 7},
                      {13, 3,11,10, 0,24,17,24, 0,29, 7},
                      {13, 3,11, 0, 0, 0,17,24, 0,29, 7}};

追加問題04 ペンシルパズル入門の例題

int[,] Q04_YokoSum = {{ 0, 8, 8, 8, 0},
                      {10,10,10,10, 0},
                      { 3, 3, 0, 8, 8},
                      { 0,29,29,29,29},
                      { 0,18,18,18, 0}};

int[,] Q04_TateSum = {{ 0,15, 4,20, 0},
                      { 4,15, 4,20, 0},
                      { 4,15, 0,20,16},
                      { 0,15,17,20,16},
                      { 0,15,17,20, 0}};

追加問題05 ペンシルパズル入門の7問目

int[,] Q05_YokoSum = {{23,23,23, 0, 0,17,17, 0, 0, 4, 4},
                      {30,30,30,30, 0,24,24,24, 0, 6, 6},
                      { 0,35,35,35,35,35, 0,10,10,10,10},
                      { 0, 0,24,24,24, 0, 0, 7, 7, 0, 0},
                      { 7, 7, 7, 0,14,14, 0,30,30,30,30},
                      { 4, 4, 0,35,35,35,35,35, 0,16,16},
                      {11,11,11,11, 0,17,17, 0,20,20,20},
                      { 0, 0, 4, 4, 0, 0,13,13,13, 0, 0},
                      {10,10,10,10, 0,15,15,15,15,15, 0},
                      { 3, 3, 0, 8, 8, 8, 0,10,10,10,10},
                      { 6, 6, 0, 0, 3, 3, 0, 0, 7, 7, 7}};

int[,] Q05_TateSum = {{16,24,34, 0, 0,23,16, 0, 0, 7, 6},
                      {16,24,34,23, 0,23,16,34, 0, 7, 6},
                      { 0,24,34,23,29,23, 0,34,13, 7, 6},
                      { 0, 0,34,23,29, 0, 0,34,13, 0, 0},
                      { 9, 6,34, 0,29,19, 0,34,13,23,24},
                      { 9, 6, 0,15,29,19,29,34, 0,23,24},
                      { 9, 6, 7,15, 0,19,29, 0,15,23,24},
                      { 0, 0, 7,15, 0, 0,29, 7,15, 0, 0},
                      { 6, 7, 7,15, 0, 7,29, 7,15, 6, 0},
                      { 6, 7, 0,15, 4, 7, 0, 7,15, 6, 4},
                      { 6, 7, 0, 0, 4, 7, 0, 0,15, 6, 4}};

追加問題06 パズルBox10の4問目

int[,] Q06_YokoSum = {{ 0, 6, 6, 6, 0, 0,16,16, 0, 6, 6, 6, 0,11,11},
                      {29,29,29,29, 0,23,23,23, 0,22,22,22,22,22,22},
                      {12,12, 0,28,28,28,28,28,28,28, 0,10,10,10, 0},
                      { 0,15,15,15,15,15, 0,21,21,21,21,21, 0,14,14},
                      { 7, 7, 7, 0,29,29,29,29, 0,13,13, 0,24,24,24},
                      {10,10, 0,16,16, 0, 7, 7, 7, 0,29,29,29,29, 0},
                      {41,41,41,41,41,41,41, 0,15,15,15,15,15, 0, 0},
                      { 0,10,10, 0, 0,10,10, 0, 8, 8, 0, 0,10,10, 0},
                      { 0, 0,30,30,30,30,30, 0,29,29,29,29,29,29,29},
                      { 0,30,30,30,30, 0, 6, 6, 6, 0, 4, 4, 0,10,10},
                      { 6, 6, 6, 0, 4, 4, 0,10,10,10,10, 0,23,23,23},
                      {17,17, 0,15,15,15,15,15, 0,34,34,34,34,34, 0},
                      { 0,13,13,13, 0,42,42,42,42,42,42,42, 0, 7, 7},
                      {38,38,38,38,38,38, 0, 7, 7, 7, 0,10,10,10,10},
                      {16,16, 0, 6, 6, 6, 0, 6, 6, 0, 0,24,24,24, 0}};

int[,] Q06_TateSum = {{ 0,43,10,11, 0, 0,24,39, 0,15, 3,10, 0,39, 4},
                      {13,43,10,11, 0,21,24,39, 0,15, 3,10,10,39, 4},
                      {13,43, 0,11,35,21,24,39, 6,15, 0,10,10,39, 0},
                      { 0,43, 4,11,35,21, 0,39, 6,15,23,10, 0,39,16},
                      { 7,43, 4, 0,35,21,21,39, 0,15,23, 0,34,39,16},
                      { 7,43, 0,17,35, 0,21,39,21, 0,23,10,34,39, 0},
                      { 7,43,16,17,35,24,21, 0,21, 7,23,10,34, 0, 0},
                      { 0,43,16, 0, 0,24,21, 0,21, 7, 0, 0,34,43, 0},
                      { 0, 0,16,17,17,24,21, 0,21, 7,15, 3,34,43,23},
                      { 0,38,16,17,17, 0,21,22,21, 0,15, 3, 0,43,23},
                      {10,38,16, 0,17,20, 0,22,21,18,15, 0,16,43,23},
                      {10,38, 0,11,17,20,13,22, 0,18,15,21,16,43, 0},
                      { 0,38,16,11, 0,20,13,22, 7,18,15,21, 0,43, 4},
                      {14,38,16,11, 8,20, 0,22, 7,18, 0,21,10,43, 4},
                      {14,38, 0,11, 8,20, 0,22, 7, 0, 0,21,10,43, 0}};

解説

カックロ分解表を最初に作成しておくことにより、計算量を削減してます。

HashSetジェネリックで、
マスに埋める候補となる数値の集合に対して、
和集合演算や差集合演算や積集合演算を行ってます。