遊び倒すガイド 上級編 バッタのジャンプの場合の数

問題

6枚のタイルが横1列に並んでいる。
いま、左端のタイル（S）上に1匹のバッタがいる。
バッタは次のルールにしたがってジャンプを繰り返し、右端のタイル（G）に向かう。
●バッタは右または左方向にジャンプする。任意の枚数のタイルを飛び越え、他のタイルに着地する。
●バッタはジャンプすると、次はその反対方向にジャンプする。
●バッタはGに到着する前に、他のすべてのタイルにちょうど1度ずつ着地する。Sは始めから着地済みとみなす。

このようにGへ到着する仕方は、下記の5通りある。


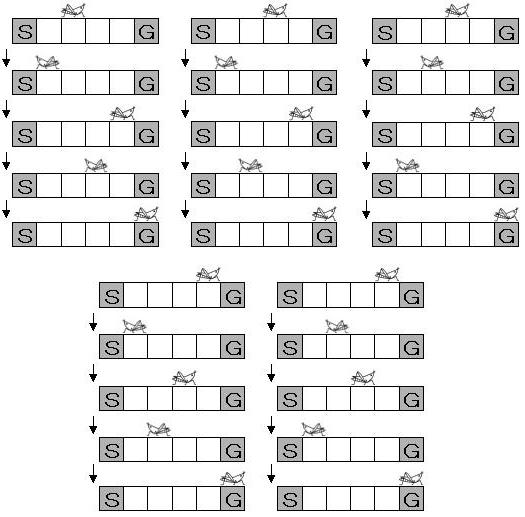20枚のタイルが横1列に並ぶとき、Gへ到着する仕方は何通りあるか？

プロジェクトオイラーを遊び倒すガイド (上級編)

ソース(動的計画法)

using System;
using System.Linq;

class Program
{
    //const long TileCnt = 6 - 2;
    const long TileCnt = 20 - 2;

    static void Main()
    {
        //場合の数[左のタイル数,右のタイル数]なDP表
        long[,] PrevDP = new long[TileCnt + 1, TileCnt + 1];
        PrevDP[0, TileCnt] = 1;

        for (long I = 1; I <= TileCnt; I++) {
            long[,] CurrDP = new long[TileCnt + 1, TileCnt + 1];

            for (long LeftTileCnt = 0; LeftTileCnt <= TileCnt; LeftTileCnt++) {
                for (long RightTileCnt = 0; RightTileCnt <= TileCnt; RightTileCnt++) {

                    long CurrPetternCnt = PrevDP[LeftTileCnt, RightTileCnt];
                    if (CurrPetternCnt == 0) continue;

                    //左にジャンプする場合
                    if (I % 2 == 0 && LeftTileCnt > 0) {
                        for (long JumpedTileCnt = 0;
                                  JumpedTileCnt <= LeftTileCnt - 1; JumpedTileCnt++) {
                            CurrDP[LeftTileCnt - JumpedTileCnt - 1,
                                   RightTileCnt + JumpedTileCnt] += CurrPetternCnt;
                        }
                    }

                    //右にジャンプする場合
                    if (I % 2 == 1 && RightTileCnt > 0) {
                        for (long JumpedTileCnt = 0;
                                  JumpedTileCnt <= RightTileCnt - 1; JumpedTileCnt++) {
                            CurrDP[LeftTileCnt + JumpedTileCnt,
                                   RightTileCnt - JumpedTileCnt - 1] += CurrPetternCnt;
                        }
                    }
                }
            }
            Console.WriteLine("{0}回目のDPの結果", I);
            PrintDP(CurrDP);

            PrevDP = CurrDP;
        }
        Console.WriteLine("Answer={0}", PrevDP.Cast<long>().Sum());
    }

    static void PrintDP(long[,] pDP)
    {
        var sb = new System.Text.StringBuilder();
        for (long I = 0; I <= pDP.GetUpperBound(0); I++) {
            for (long J = 0; J <= pDP.GetUpperBound(1); J++) {
                if (pDP[I, J] == 0) continue;
                sb.AppendFormat("左のタイル{0}個で右のタイル{1}個の場合の数={2}",
                    I, J, pDP[I, J]);
                sb.AppendLine();
            }
        }
        Console.WriteLine(sb.ToString());
    }
}

ソース(ジグザグ数を求める)

using System;
using System.Collections.Generic;
using System.Linq;

class Program
{
    //const int TileCnt = 6;
    const int TileCnt = 20;

    static void Main()
    {
        var ZigZagValDict = new Dictionary<int, List<long>>();
        for (int N = 1; N <= TileCnt - 1; N++) {
            if (N == 1) {
                ZigZagValDict.Add(1, new List<long>() { 1 });
                continue;
            }
            var WillAddList = new List<long>() { 0 };
            long CurrSum = 0;

            for (int I = ZigZagValDict[N - 1].Count - 1; 0 <= I; I--) {
                CurrSum += ZigZagValDict[N - 1][I];
                WillAddList.Add(CurrSum);
            }
            ZigZagValDict.Add(N, WillAddList);
        }
        Console.WriteLine("Answer={0}", ZigZagValDict[TileCnt - 1].Last());
    }
}

実行結果

16回目のDPの結果
左のタイル0個で右のタイル2個の場合の数=1372696498127
左のタイル1個で右のタイル1個の場合の数=1032183177314
左のタイル2個で右のタイル0個の場合の数=562021682744

17回目のDPの結果
左のタイル0個で右のタイル1個の場合の数=1372696498127
左のタイル1個で右のタイル0個の場合の数=2404879675441

18回目のDPの結果
左のタイル0個で右のタイル0個の場合の数=2404879675441

Answer=2404879675441

解説

三角形を経由して、ジグザグ数を求めると計算量が少ないです。

オイラー数とタンジェント数(1)
ジグザグ数(zigzag number)
オイラー数はzig number、タンジェント数はzag numberとも呼ばれ、下図の三角形により生成される。その規則は
・頂点は1であり、0から始めて右左右左とジグザグに値を決める
・進行方向の斜め上の数を加えて次の数を作る(例:10+4=14)



この数は下図の折れ線で示す交代順列の個数に等しい。