結城さん問題01 マヨイドーロ

■■■マヨイドーロ■■■

以下の道をマヨイドーロと呼びます。



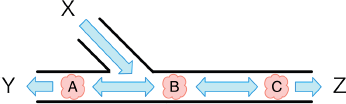Xがマヨイドーロの入口で、YとZが出口になります。
A,B,Cをマヨイと呼びます。
マヨイは「そのまま直進してもいいけれど、進む向きを反転してもいい地点」を表します。

入口Xからマヨイドーロに入った人は、最初は必ずZ向きに進み、Bに着きます。
その後、Xへ戻ることはできず、マヨイドーロの中を通過して、YかZの出口から出ます。

たとえばアリスは、マヨイドーロをこんなふうに通りました。
●Xから入り、Bに着いた。
●反転してYに向かい、Aに着いた。
●反転してZに向かい、Bに着いた。
●直進してZに向かい、Cに着いた。
●直進してZから出た。
つまりアリスは、反転を2回行って、
X→B→A→B→C→Z
というルートを通ったことになります。

またボブは、マヨイドーロをこんなふうに通りました。
●Xから入り、Bに着いた。
●直進してZに向かい、Cに着いた。
●反転してYに向かい、Bに着いた。
●直進してYに向かい、Aに着いた。
●直進してYから出た。
つまりボブは、反転を1回行って、
X→B→C→B→A→Y
というルートを通ったことになります。

■■■NとP■■■

Nを「反転回数の上限」とします。
言い換えるならNは「その回数までは反転してかまわないという数」です。
Pを「Xから入ってYから出るルートの種類の数」とします。

N=0の例
もしもNが0の場合には、直進しかできませんので、
●X→B→C→Z
という、Zから出るルートしかありません。したがって、Yから出るルートの総数Pは、0になります。

N=1の例
もしもNが1の場合、Yから出るルートは、
●X→B→C→B→A→Y
●X→B→A→Y
という2種類があるので、Pは2になります。

N=4の例
もしもNが4の場合、Yから出るルートは、
●X→B→C→B→A→Y
●X→B→C→B→A→B→C→B→A→Y
●X→B→C→B→A→B→A→Y
●X→B→C→B→C→B→A→Y
●X→B→A→Y
●X→B→A→B→C→B→A→Y
●X→B→A→B→A→Y
という7種類があるので、Pは7になります。

■■■問題■■■

Nが与えられたとき、Pを出力するプログラムを書いてください。

C++のソース

#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <string>
#include <vector>

std::string InputPattern = "Input1";

std::vector<std::string> GetInputValues()
{
    std::vector<std::string> InputValuesVect;

    if (InputPattern == "Input1") {
        InputValuesVect.push_back("1");
        //2
    }
    else if (InputPattern == "Input2") {
        InputValuesVect.push_back("4");
        //7
    }
    else { //実際の入力
        while (true) {
            std::string wkStr;
            std::getline(std::cin, wkStr);
            if (std::cin.eof()) break;
            InputValuesVect.push_back(wkStr.c_str());
        }
    }
    return InputValuesVect;
}

class CppBigInteger{
    static const int UB = 450;
    int mNumArr[UB + 1];

public:
    CppBigInteger()
    {
        for (int I = 0; I <= UB; I++) {
            mNumArr[I] = 0;
        }
    }

    void Add(int pNum)
    {
        int CurrInd = 0;
        while (pNum > 0) {
            mNumArr[CurrInd++] += pNum % 10;
            pNum /= 10;
        }
        KetaAgariSyori();
    }

    void Add(CppBigInteger pIns)
    {
        for (int I = 0; I <= UB; I++) {
            mNumArr[I] += pIns.mNumArr[I];
        }
        KetaAgariSyori();
    }

    //文字列で表現
    std::string DeriveStr()
    {
        std::string WillOut;
        bool FoundNonZero = false;
        for (int I = UB; 0 <= I; I--) {
            if (mNumArr[I] != 0) FoundNonZero = true;
            if (FoundNonZero){
                char wkChar[100] = "\0";
                sprintf(wkChar, "%d", mNumArr[I]);
                WillOut += wkChar;
            }
        }
        if (FoundNonZero == false) return "0";
        return WillOut;
    }

private:
    //桁上がりを処理
    void KetaAgariSyori()
    {
        for (int I = 0; I <= UB; I++) {
            if (mNumArr[I] >= 10) {
                mNumArr[I + 1] += mNumArr[I] / 10;
                mNumArr[I] %= 10;
            }
        }
    }
};

int main()
{
    std::vector<std::string> InputVect = GetInputValues();
    int N = atoi(InputVect.at(0).c_str());
    std::vector<CppBigInteger> PatternCntVect;

    CppBigInteger Kou1; Kou1.Add(1);
    PatternCntVect.push_back(Kou1);

    CppBigInteger Kou2; Kou2.Add(2);
    PatternCntVect.push_back(Kou2);

    for (int I = 2; I <= N; I++) {
        CppBigInteger wkKou;
        wkKou.Add(PatternCntVect.at(I - 2));
        wkKou.Add(PatternCntVect.at(I - 1));
        PatternCntVect.push_back(wkKou);

        //printf("%d回反転して、出口に到達する場合の数は%s\n",
        //  I, PatternCntVect.at(I).DeriveStr().c_str());
    }
    CppBigInteger PatternCntSum;
    for (int I = 1; I <= N; I += 2) {
        PatternCntSum.Add(PatternCntVect.at(I));
    }
    printf("%s\n", PatternCntSum.DeriveStr().c_str());
}

解説

下記の考えによる漸化式を使ってます。

0回反転で最初の向きの出口に到達は1通り
1回反転で最初の逆向きの出口に到達は2通り

n回 (N >= 2 ) 反転で出口に到達は、
最初に反転したら、次は反転しかないので、
n-2回反転で最初の向きの出口に到達する場合の数
最初に反転しなかったら、次は反転しかないので、
n-1回反転で最初の逆向きの出口に到達する場合の数