using System;
using System.Collections.Generic;
using System.Linq;
class Program
{
static string InputPattern = "Input1";
static List<string> GetInputList()
{
var WillReturn = new List<string>();
if (InputPattern == "Input1") {
WillReturn.Add("4 4");
WillReturn.Add("...G");
WillReturn.Add(".RR.");
WillReturn.Add(".RR.");
WillReturn.Add("S...");
//3
//例えば(4, 1) -> (2, 2) -> (3, 3) -> (1, 4)
//と移動すると最短手数でクリアできます。
//このとき、駒は ナイト -> ミニビショップ -> ナイト と変化します。
}
else if (InputPattern == "Input2") {
WillReturn.Add("3 4");
WillReturn.Add("...G");
WillReturn.Add("....");
WillReturn.Add("S...");
//3
//この例ではチェス盤に赤いマスはありません。
//例えば (3, 1) -> (1, 2) -> (3, 3) -> (1, 4)
//と移動すると最短手数でクリアできます。
}
else if (InputPattern == "Input3") {
WillReturn.Add("3 3");
WillReturn.Add(".R.");
WillReturn.Add("RGR");
WillReturn.Add("SR.");
//-1
//この例では、駒はゴール地点に到達することができません。
}
else {
string wkStr;
while ((wkStr = Console.ReadLine()) != null) WillReturn.Add(wkStr);
}
return WillReturn;
}
static int UB_X;
static int UB_Y;
struct JyoutaiDef
{
internal int Level;
internal int CurrX;
internal int CurrY;
internal bool IsKnight;
}
static void Main()
{
List<string> InputList = GetInputList();
int[] wkArr = InputList[0].Split(' ').Select(X => int.Parse(X)).ToArray();
int H = wkArr[0];
int W = wkArr[1];
char[,] BanArr = new char[W, H];
UB_X = W - 1;
UB_Y = H - 1;
int StaX = -1, StaY = -1, GoalX = -1, GoalY = -1;
for (int X = 0; X <= UB_X; X++) {
for (int Y = 0; Y <= UB_Y; Y++) {
BanArr[X, Y] = InputList[Y + 1][X];
if (BanArr[X, Y] == 'S') {
StaX = X; StaY = Y;
}
if (BanArr[X, Y] == 'G') {
GoalX = X; GoalY = Y;
}
}
}
var Que = new Queue<JyoutaiDef>();
JyoutaiDef WillEnqueue;
WillEnqueue.Level = 0;
WillEnqueue.CurrX = StaX;
WillEnqueue.CurrY = StaY;
WillEnqueue.IsKnight = true;
Que.Enqueue(WillEnqueue);
var VisitedSet = new HashSet<int>();
VisitedSet.Add(GetHash(WillEnqueue));
while (Que.Count > 0) {
JyoutaiDef Dequeued = Que.Dequeue();
//クリア判定
if (Dequeued.CurrX == GoalX && Dequeued.CurrY == GoalY) {
Console.WriteLine(Dequeued.Level);
return;
}
Action<int, int> EnqueueSyori = (pNewX, pNewY) =>
{
if (pNewX < 0 || UB_X < pNewX) return;
if (pNewY < 0 || UB_Y < pNewY) return;
WillEnqueue.Level = Dequeued.Level + 1;
WillEnqueue.CurrX = pNewX;
WillEnqueue.CurrY = pNewY;
WillEnqueue.IsKnight = Dequeued.IsKnight;
if (BanArr[pNewX, pNewY] == 'R') {
WillEnqueue.IsKnight = !WillEnqueue.IsKnight;
}
//再訪は不可
if (VisitedSet.Add(GetHash(WillEnqueue)) == false)
return;
Que.Enqueue(WillEnqueue);
};
if (Dequeued.IsKnight) {
EnqueueSyori(Dequeued.CurrX - 1, Dequeued.CurrY - 2);
EnqueueSyori(Dequeued.CurrX + 1, Dequeued.CurrY - 2);
EnqueueSyori(Dequeued.CurrX - 2, Dequeued.CurrY - 1);
EnqueueSyori(Dequeued.CurrX + 2, Dequeued.CurrY - 1);
EnqueueSyori(Dequeued.CurrX - 2, Dequeued.CurrY + 1);
EnqueueSyori(Dequeued.CurrX + 2, Dequeued.CurrY + 1);
EnqueueSyori(Dequeued.CurrX - 1, Dequeued.CurrY + 2);
EnqueueSyori(Dequeued.CurrX + 1, Dequeued.CurrY + 2);
}
else {
EnqueueSyori(Dequeued.CurrX - 1, Dequeued.CurrY - 1);
EnqueueSyori(Dequeued.CurrX + 1, Dequeued.CurrY - 1);
EnqueueSyori(Dequeued.CurrX - 1, Dequeued.CurrY + 1);
EnqueueSyori(Dequeued.CurrX + 1, Dequeued.CurrY + 1);
}
}
Console.WriteLine(-1);
}
//現在位置とIsKnightからハッシュ値を求める
static int GetHash(JyoutaiDef pJyoutai)
{
int Hash = pJyoutai.CurrX * 10000;
Hash += pJyoutai.CurrY * 10;
Hash += (pJyoutai.IsKnight ? 1 : 0);
return Hash;
}
}
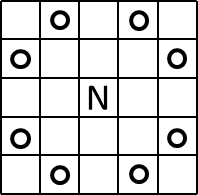
さて、あなたは最短何手でこのゲームをクリアすることができるでしょうか?