ABC-058-D 井井井 / ###

■■■問題■■■

2次元平面上にx軸と平行な直線がm本とy軸と平行な直線がn本引いてあります。
x軸と平行な直線のうち下からi番目は y=yi で表せます。
y軸と平行な直線のうち左からi番目は x=xi で表せます。

この中に存在しているすべての長方形についてその面積を求め、
合計を1000000007で割ったあまりを出力してください。

つまり、1 <= i < j <= n と 1 <= k < l <= m を満たすすべての組 (i,j,k,l) について、
直線 x=xi, x=xj, y=yk, y=yl で囲まれる 長方形の面積を求め、
合計を1000000007で割ったあまりを出力してください。

■■■入力■■■

n m
x1 x2 ・・・ xn
y1 y2 ・・・ ym

●2 <= n,m <= 10万
●-10億 <= x1 < ・・・ < xn <= 10億
●-10億 <= y1 < ・・・ < ym <= 10億
●xi,yi は整数である

■■■出力■■■

長方形の面積の合計を1000000007で割ったあまりを1行に出力せよ。

■■■サンプルケースのイメージ■■■

■入出力例1のイメージ■

この入力を図にすると、以下のようになります。



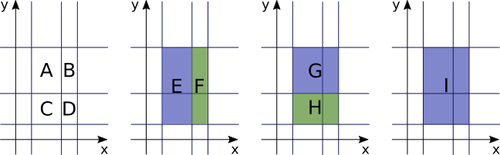
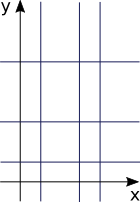長方形 A,B, ・・・ ,I それぞれの面積を合計すると60になります。

C#のソース

using System;
using System.Collections.Generic;
using System.Linq;

class Program
{
    const long Hou = 1000000007;

    static string InputPattern = "Input1";

    static List<string> GetInputList()
    {
        var WillReturn = new List<string>();

        if (InputPattern == "Input1") {
            WillReturn.Add("3 3");
            WillReturn.Add("1 3 4");
            WillReturn.Add("1 3 6");
            //60
        }
        else if (InputPattern == "Input2") {
            WillReturn.Add("6 5");
            WillReturn.Add("-790013317 -192321079 95834122 418379342 586260100 802780784");
            WillReturn.Add("-253230108 193944314 363756450 712662868 735867677");
            //835067060
        }
        else {
            string wkStr;
            while ((wkStr = Console.ReadLine()) != null) WillReturn.Add(wkStr);
        }
        return WillReturn;
    }

    static void Main()
    {
        List<string> InputList = GetInputList();
        int[] XArr = InputList[1].Split(' ').Select(A => int.Parse(A)).ToArray();
        int[] YArr = InputList[2].Split(' ').Select(A => int.Parse(A)).ToArray();

        long SenbunSumX = DeriveSenbunSum(XArr);
        long SenbunSumY = DeriveSenbunSum(YArr);

        long Answer = SenbunSumX * SenbunSumY;
        Answer %= Hou;
        Console.WriteLine(Answer);
    }

    //座標の配列を引数として、作成可能な線分の長さの総和を返す
    static long DeriveSenbunSum(int[] pArr)
    {
        int UB = pArr.GetUpperBound(0);
        long SenbunSum = 0;
        for (int I = 0; I <= UB; I++) {
            long CurrPos = pArr[I] % Hou;
            int KeisuuMinus = I;
            int KeisuuPlus = UB - I;
            SenbunSum += -CurrPos * KeisuuMinus;
            SenbunSum %= Hou;
            SenbunSum += CurrPos * KeisuuPlus;
            SenbunSum %= Hou;
        }
        return SenbunSum;
    }
}

解説

数直線に点A,B,C,D,Eがあるとし、
任意の2点からなる線分の長さの総合計を求めるとすると、
点Aは、線分の始点となるのが4回、終点となるのが0回
点Bは、線分の始点となるのが3回、終点となるのが1回
点Cは、線分の始点となるのが2回、終点となるのが2回
点Dは、線分の始点となるのが1回、終点となるのが3回
点Eは、線分の始点となるのが0回、終点となるのが4回
ですので、

線分の長さの総合計は、
A*(-4) + B*(-2) + C*0 + D*2 + E*4
で求まります。

そして、積の法則の感覚を使って、
X方向の線分の長さの総合計と
Y方向の線分の長さの総合計を掛け算すれば解となります。