CODE FESTIVAL 2015予選A D 壊れた電車

■■■問題■■■

高橋鉄道では、N両編成の電車の一部が壊れてしまったため、
M人の整備士が点検をすることになりました。

i人目の整備士ははじめ、Xi両目の車両にいます。
それぞれの整備士は、今いる車両を点検することと、隣の車両に移動することができます。
車両の点検には時間はかかりませんが、隣の車両に移動するには1分かかります。

全ての車両を少なくとも1人の整備士が点検した状態になると点検作業は終了となります。
点検作業は最短何分で終了させることができるでしょうか。

■■■入力■■■

N M
X1
X2
・
・
・
XM

●1行目には、2つの整数 N(1 <= N <= 10億),M(1 <= M <= 10万,M <= N) が空白区切りで与えられる。
  これは、電車がN両の車両からなり、整備士がM人いることを表す。
●2行目からのM行には、整備士の情報が与えられる。
  このうち i(1 <= i <= M) 行目には、整数 Xi(1 <= Xi <= N) が与えられる。
  これは、i人目の整備士がはじめ Xi 両目の車両にいることを表す。
  ただし、Xiは全て相異なることが保証される。
  また、整備士の情報は1両目の車両に近い順に与えられる、
  つまり Xj<Xj+1(1 <= j <= M-1) であることが保証される。

■■■出力■■■

点検作業にかかる時間の最小値を分単位で1行に出力せよ。
出力の末尾に改行を入れること。

■■■サンプルケースのイメージ■■■

Input1 下の図のように整備士が移動すれば3分で点検作業を終了させることができます。

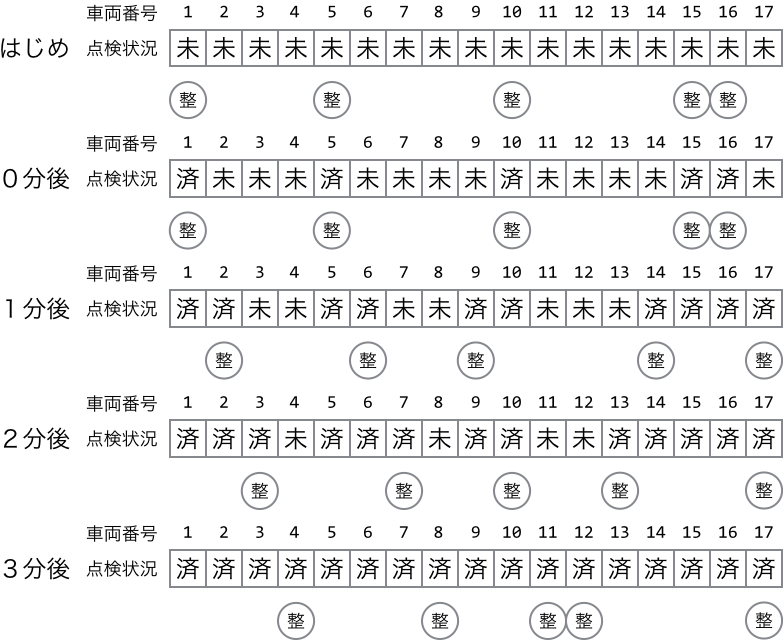
C#のソース

using System;
using System.Collections.Generic;
using System.Linq;

class Program
{
    static string InputPattern = "Input1";

    static List<string> GetInputList()
    {
        var WillReturn = new List<string>();

        if (InputPattern == "Input1") {
            WillReturn.Add("17 5");
            WillReturn.Add("1");
            WillReturn.Add("5");
            WillReturn.Add("10");
            WillReturn.Add("15");
            WillReturn.Add("16");
            //3
        }
        else if (InputPattern == "Input2") {
            WillReturn.Add("66 10");
            WillReturn.Add("8");
            WillReturn.Add("9");
            WillReturn.Add("16");
            WillReturn.Add("23");
            WillReturn.Add("37");
            WillReturn.Add("47");
            WillReturn.Add("51");
            WillReturn.Add("52");
            WillReturn.Add("53");
            WillReturn.Add("64");
            //8
        }
        else {
            string wkStr;
            while ((wkStr = Console.ReadLine()) != null) WillReturn.Add(wkStr);
        }
        return WillReturn;
    }

    static int N;
    static int[] XArr;

    static void Main()
    {
        List<string> InputList = GetInputList();
        N = InputList[0].Split(' ').Select(X => int.Parse(X)).First();
        XArr = InputList.Skip(1).Select(X => int.Parse(X)).ToArray();

        Console.WriteLine(ExecNibunHou());
    }

    //2分法で最小の点検時間を返す
    static int ExecNibunHou()
    {
        //0分で点検可能な場合
        if (XArr.Length == N) return 0;

        int L = 0;
        int R = N * 2;

        while (L + 1 < R) {
            int Mid = (int)(((long)L + R) / 2);
            if (CanTenken(Mid)) R = Mid;
            else L = Mid;

            //Console.WriteLine("現在のL={0},R={1}", L, R);
        }

        return R;
    }

    //K分で点検できるかを返す
    static bool CanTenken(int pK)
    {
        int MitenkenMinNo = 1;
        foreach (int EachX in XArr) {
            if (MitenkenMinNo < EachX) {
                //場合1 最小の未点検車両に到達不能の場合
                if (MitenkenMinNo < EachX - pK)
                    return false;

                //場合2 右に移動してから、最小の未点検車両に移動
                int RestHun1 = pK;
                RestHun1 -= EachX - MitenkenMinNo;
                int MitenkenMinNoKouho1 = EachX + RestHun1 / 2 + 1;

                //場合3 最小の未点検車両に移動してから、右に移動
                int RestHun2 = pK;
                RestHun2 -= (EachX - MitenkenMinNo) * 2;
                int MitenkenMinNoKouho2 = EachX + Math.Max(0, RestHun2) + 1;

                MitenkenMinNo = Math.Max(MitenkenMinNoKouho1, MitenkenMinNoKouho2);
            }

            //場合4 現在車両が点検済なら右に移動
            else {
                MitenkenMinNo = Math.Max(MitenkenMinNo, EachX + pK + 1);
            }
            //Console.WriteLine("最小の未点検車両={0}", MitenkenMinNo); 
        }
        return N < MitenkenMinNo;
    }
}

C++のソース

#include <stdio.h>
#include <valarray>

int ExecNibunHou(std::valarray<int> &pXArr);
bool CanTenken(int pK,std::valarray<int> &pXArr);
int GetMax(int p1,int p2);

int N;
int M;

int main()
{
    scanf("%d %d",&N,&M);

    std::valarray<int> XArr(M);
    for(int I=1;I<=M;I++){
        int wkInt;
        scanf("%d",&wkInt);
        XArr[I-1]=wkInt;
    }

    printf("%d\n",ExecNibunHou(XArr));

    //for (int I = 0; I <= N * 2; I++) {
    //    if (CanTenken(I) == false) continue;
    //    printf("%d\n",I);
    //    break;
    //}
}

//2分法で最小の点検時間を返す
int ExecNibunHou(std::valarray<int> &pXArr)
{
    //0分で点検可能な場合
    if ((int)pXArr.size()==N) return 0;

    int L = 0;
    int R = N * 2;

    while (L + 1 < R) {
        int Mid = ((long long)L + R) / 2;
        if (CanTenken(Mid,pXArr)) R = Mid;
        else L = Mid;

        //printf("現在のL=%d,R=%d\n",L, R);
    }

    return R;
}

//K分で点検できるかを返す
bool CanTenken(int pK,std::valarray<int> &pXArr)
{
    int MitenkenMinNo = 1;
    for(int I=0;I<=(int)pXArr.size()-1;I++){
        int EachX = pXArr[I];
        if (MitenkenMinNo < EachX) {
            //場合1 最小の未点検車両に到達不能の場合
            if (MitenkenMinNo < EachX - pK)
                return false;

            //場合2 右に移動してから、最小の未点検車両に移動
            int RestHun1 = pK;
            RestHun1 -= EachX - MitenkenMinNo;
            int MitenkenMinNoKouho1 = EachX + RestHun1 / 2 + 1;

            //場合3 最小の未点検車両に移動してから、右に移動
            int RestHun2 = pK;
            RestHun2 -= (EachX - MitenkenMinNo) * 2;
            int MitenkenMinNoKouho2 = EachX + GetMax(0, RestHun2) + 1;

            MitenkenMinNo = GetMax(MitenkenMinNoKouho1, MitenkenMinNoKouho2);
        }

        //場合4 現在車両が点検済なら右に移動
        else {
            MitenkenMinNo =GetMax(MitenkenMinNo, EachX + pK + 1);
        }
        //printf("最小の未点検車両=%d\n",MitenkenMinNo);
    }
    return N < MitenkenMinNo;
}

int GetMax(int p1,int p2)
{
    return (p1<p2 ? p2 : p1);
}

解説

左の車両から順番に点検していくようにして、
2分法で最小の分数を求めてます。