次のゲームは, 組み合わせゲーム理論の古典的な例である:
2人のプレイヤーが, 一列に並んだn個の白い正方形から開始して, 交互にターンを行う.
各ターンでは, プレイヤーは2つの隣り合う白い正方形を選び, 黒で塗る.
最初に色を塗ることができなくなったプレイヤーが負けとなる.
●n=1の場合, 有効な手はないため, 先手が自動的に負けとなる.
●n=2の場合, 有効な手は1つのみであり, その後, 後手が負けとなる.
●n=3の場合, 有効な手は2つあるが, どちらも後手が負ける状況となる.
●n=4の場合, 有効な手は先手に3つある; 先手は中央の2つの正方形を塗ると勝利できる.
●n=5の場合, 有効な手は先手に4つある(下図に赤で示す);
しかしいずれを選んでも, 後手(青)が勝利する.
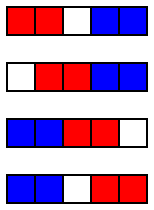したがって, 1 <= n <= 5 に対し,先手必勝となるnの値は3個ある.
同様に, 1 <= n <= 50 に対し,先手必勝となるnの値は40個ある.
1 <= n <= 100万に対し,先手必勝となるnの値は何個あるか.