トップページに戻る    次のC#のサンプルへ    前のC#のサンプルへ

Cマガ電脳クラブ(第045回) 鴛鴦の遊び

問題

『勘者御伽双紙』(1743年)をヒントに出題する。
まずは白黒3個を交互に並べて出発点とする。

そのうちの隣合う2個を選び、隣合わせのまま並行に移動する。
移動する際、少なくとも一方の石がほかの碁石に接しなければならない(つまり、宙ぶらりんな位置には移動できない)。
これを繰り返して、白3個と黒3個を隣合わせにそれぞれ連続して並べたら完成である。

その解答をFig.1にあげた。いちばんうえが出発点。そのうちのアンダーラインの2個を移動して2段目にする。
以下同様に、4段目まで3手で完成している。

さて、白黒6個を交互に並べて出発点(Fig.2)とし、
同じルールで白と黒各6個をそれぞれ連続して並べる(Fig.3：白黒が入れ換わった形でもよい)には最低何手かかるか。
ただし、ここでは「隣り合う2個を」移動する代わりに、「隣合う3個」を移動することにする。
移動の手順を一通りだけ書いてほしい。

このパズル、白石と黒石が仲よく並ぶさまから、鴛鴦(おしどり)、エンオウの遊びと呼ばれた。

ソース

using System;
using System.Collections.Generic;
using System.Linq;

class Program
{
    enum MasuDef
    {
        Kuuhaku = 0,
        White = 1,
        Black = 2
    }

    struct JyoutaiDef
    {
        internal MasuDef[] IshiArr;
        internal List<MasuDef[]> Log;
    }

    const int WhiteCnt = 6;
    const int BlackCnt = 6;

    static System.Diagnostics.Stopwatch sw = System.Diagnostics.Stopwatch.StartNew();

    static void Main()
    {
        for (int Depth = 1; Depth <= 10; Depth++) {
            Console.WriteLine("深さ制限={0}で解を検証中。経過時間={1}", Depth, sw.Elapsed);
            if (ExecDFS(Depth)) return;
        }
    }

    //深さ制限を引数として深さ優先探索を行う
    static bool ExecDFS(int pDepthMax)
    {
        bool WillReturn = false;

        var stk = new Stack<JyoutaiDef>();

        JyoutaiDef WillPush;
        var WKList = new List<MasuDef>();
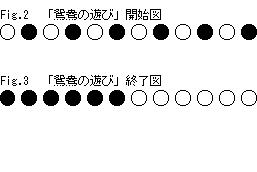
        WKList.AddRange(Enumerable.Repeat(MasuDef.Kuuhaku, 12));
        for (int I = 1; I <= 6; I++)
            WKList.AddRange(new MasuDef[] { MasuDef.White, MasuDef.Black });
        WKList.AddRange(Enumerable.Repeat(MasuDef.Kuuhaku, 12));
        WillPush.IshiArr = WKList.ToArray();
        WillPush.Log = new List<MasuDef[]>() { WillPush.IshiArr };
        stk.Push(WillPush);

        while (stk.Count > 0) {
            JyoutaiDef Popped = stk.Pop();

            if (pDepthMax < Popped.Log.Count + CalcNeedMinTesuu(Popped.IshiArr)) continue;

            if (IsAnswer(Popped.IshiArr)) {
                Console.WriteLine("解を発見。経過時間={0}", sw.Elapsed);

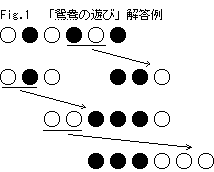
                PrintLog(Popped.Log);
                return true;
            }

            Action<int, int> PushSyori = (pMinP, pMaxP) =>
            {
                //既存の配置だったら枝切り
                if (Popped.Log.Exists(X => X.SequenceEqual(WillPush.IshiArr))) {
                    return;
                }

                WillPush.Log = new List<MasuDef[]>(Popped.Log);
                WillPush.Log.Add(WillPush.IshiArr);

                stk.Push(WillPush);
            };

            MasuDef[] WK_P = Popped.IshiArr;

            //3マスの空白への移動
            for (int I = 0; I <= WK_P.GetUpperBound(0) - 2; I++) {
                bool Has3Space = false;
                if (WK_P[I] == MasuDef.Kuuhaku &&
                    WK_P[I + 1] == MasuDef.Kuuhaku &&
                    WK_P[I + 2] == MasuDef.Kuuhaku) {
                    Has3Space = true;
                }
                if (Has3Space == false) continue;

                //移動する際、少なくとも一方の石がほかの碁石に接しなければならない
                if (HasGoishi(WK_P, I - 1) == false &&
                    HasGoishi(WK_P, I + 3) == false) continue;

                for (int J = 0; J <= WK_P.GetUpperBound(0) - 2; J++) {
                    if (WK_P[J] != MasuDef.Kuuhaku &&
                        WK_P[J + 1] != MasuDef.Kuuhaku &&
                        WK_P[J + 2] != MasuDef.Kuuhaku) {
                        WillPush.IshiArr = (MasuDef[])WK_P.Clone();
                        WillPush.IshiArr[I] = WK_P[J];
                        WillPush.IshiArr[I + 1] = WK_P[J + 1];
                        WillPush.IshiArr[I + 2] = WK_P[J + 2];
                        WillPush.IshiArr[J] = MasuDef.Kuuhaku;
                        WillPush.IshiArr[J + 1] = MasuDef.Kuuhaku;
                        WillPush.IshiArr[J + 2] = MasuDef.Kuuhaku;

                        PushSyori(I, I + 2);
                    }
                }
            }

            //2マスの空白への移動
            for (int I = 0; I <= WK_P.GetUpperBound(0) - 4; I++) {
                if (HasGoishi(WK_P, I - 1) &&
                    WK_P[I] == MasuDef.Kuuhaku &&
                    WK_P[I + 1] == MasuDef.Kuuhaku &&
                    WK_P[I + 2] != MasuDef.Kuuhaku &&
                    WK_P[I + 3] != MasuDef.Kuuhaku &&
                    WK_P[I + 4] != MasuDef.Kuuhaku) {

                    WillPush.IshiArr = (MasuDef[])WK_P.Clone();
                    WillPush.IshiArr[I] = WK_P[I + 1];
                    WillPush.IshiArr[I + 1] = WK_P[I + 2];
                    WillPush.IshiArr[I + 2] = WK_P[I + 3];
                    WillPush.IshiArr[I + 3] = MasuDef.Kuuhaku;
                    WillPush.IshiArr[I + 4] = MasuDef.Kuuhaku;
                    PushSyori(I, I + 2);
                }
                if (WK_P[I] != MasuDef.Kuuhaku &&
                    WK_P[I + 1] != MasuDef.Kuuhaku &&
                    WK_P[I + 2] != MasuDef.Kuuhaku &&
                    WK_P[I + 3] == MasuDef.Kuuhaku &&
                    WK_P[I + 4] == MasuDef.Kuuhaku &&
                    HasGoishi(WK_P, I + 5)) {
                    WillPush.IshiArr = (MasuDef[])WK_P.Clone();
                    WillPush.IshiArr[I + 4] = WK_P[I + 3];
                    WillPush.IshiArr[I + 3] = WK_P[I + 2];
                    WillPush.IshiArr[I + 2] = WK_P[I + 1];
                    WillPush.IshiArr[I + 1] = MasuDef.Kuuhaku;
                    WillPush.IshiArr[I] = MasuDef.Kuuhaku;
                    PushSyori(I + 2, I + 4);
                }
            }

            //1マスの空白への移動
            for (int I = 0; I <= WK_P.GetUpperBound(0) - 3; I++) {
                if (HasGoishi(WK_P, I - 1) &&
                    WK_P[I] == MasuDef.Kuuhaku &&
                    WK_P[I + 1] != MasuDef.Kuuhaku &&
                    WK_P[I + 2] != MasuDef.Kuuhaku &&
                    WK_P[I + 3] != MasuDef.Kuuhaku) {

                    WillPush.IshiArr = (MasuDef[])WK_P.Clone();
                    WillPush.IshiArr[I] = WK_P[I + 1];
                    WillPush.IshiArr[I + 1] = WK_P[I + 2];
                    WillPush.IshiArr[I + 2] = WK_P[I + 3];
                    WillPush.IshiArr[I + 3] = MasuDef.Kuuhaku;
                    PushSyori(I, I + 2);
                }
                if (WK_P[I] != MasuDef.Kuuhaku &&
                    WK_P[I + 1] != MasuDef.Kuuhaku &&
                    WK_P[I + 2] != MasuDef.Kuuhaku &&
                    WK_P[I + 3] == MasuDef.Kuuhaku &&
                    HasGoishi(WK_P, I + 4)) {
                    WillPush.IshiArr = (MasuDef[])WK_P.Clone();
                    WillPush.IshiArr[I + 3] = WK_P[I + 2];
                    WillPush.IshiArr[I + 2] = WK_P[I + 1];
                    WillPush.IshiArr[I + 1] = WK_P[I];
                    WillPush.IshiArr[I] = MasuDef.Kuuhaku;
                    PushSyori(I + 1, I + 3);
                }
            }
        }
        return WillReturn;
    }

    //移動する際、少なくとも一方の石がほかの碁石に接しなければならない
    static bool IsRinsetu(MasuDef[] pIshiArr, int pMinP, int pMaxP)
    {
        if (0 <= pMinP - 1 &&
            pIshiArr[pMinP - 1] != MasuDef.Kuuhaku) return true;
        if (pMaxP + 1 <= pIshiArr.GetUpperBound(0) &&
            pIshiArr[pMaxP + 1] != MasuDef.Kuuhaku) return true;
        return false;
    }

    //解に到達したかを判定
    static bool IsAnswer(MasuDef[] pIshiArr)
    {
        var Query = pIshiArr.SkipWhile(X => X == MasuDef.Kuuhaku)
                            .TakeWhile(X => X != MasuDef.Kuuhaku);

        var WK1 = Enumerable.Repeat(MasuDef.White, WhiteCnt);
        var WK2 = Enumerable.Repeat(MasuDef.Black, BlackCnt);

        return Query.SequenceEqual(WK1.Concat(WK2)) ||
               Query.SequenceEqual(WK2.Concat(WK1));
    }

    //移動のログを表示
    static void PrintLog(List<MasuDef[]> pLog)
    {
        int Level = 0;
        var sb = new System.Text.StringBuilder();
        foreach (MasuDef[] AnyArr in pLog) {
            sb.AppendFormat("LV{0,2}=", ++Level);
            foreach (MasuDef AnyMasu in AnyArr) {
                if (AnyMasu == MasuDef.Kuuhaku) sb.Append('　');
                if (AnyMasu == MasuDef.White) sb.Append('○');
                if (AnyMasu == MasuDef.Black) sb.Append('●');
            }
            sb.AppendLine();
        }
        Console.WriteLine(sb.ToString());
    }

    //碁石の存在チェック
    static bool HasGoishi(MasuDef[] pIshiArr, int pTargetP)
    {
        if (pTargetP < 0 || pIshiArr.GetUpperBound(0) < pTargetP) return false;
        return pIshiArr[pTargetP] != MasuDef.Kuuhaku;
    }

    //必要な最低手数を求める
    static int CalcNeedMinTesuu(MasuDef[] pIshiArr)
    {
        int WhiteSeqCnt = 0;
        int BlackSeqCnt = 0;

        for (int I = 0; I <= pIshiArr.GetUpperBound(0); I++) {
            if (pIshiArr[I] == MasuDef.White &&
                (I == 0 || pIshiArr[I - 1] != MasuDef.White))
                WhiteSeqCnt++;
            if (pIshiArr[I] == MasuDef.Black &&
                (I == 0 || pIshiArr[I - 1] != MasuDef.Black))
                BlackSeqCnt++;
        }
        return Math.Max(WhiteSeqCnt - 1, BlackSeqCnt - 1);
    }
}

実行結果

深さ制限=1で解を検証中
深さ制限=2で解を検証中
深さ制限=3で解を検証中
深さ制限=4で解を検証中
深さ制限=5で解を検証中
深さ制限=6で解を検証中
深さ制限=7で解を検証中
深さ制限=8で解を検証中
解を発見
LV 1=　　　　　　　　　　　　○●○●○●○●○●○●
LV 2=　　　　　　　　　　　　○●○●○●○●○　　　●○●
LV 3=　　　　　　　　　　　　　　　●○●○●○○●○●○●
LV 4=　　　　　　　　　　　　　　　●○●○　　　●○●○●●○○
LV 5=　　　　　　　　　　　　　　　●○●○○●●●○●　　　○○
LV 6=　　　　　　　　　　　　　　　●○　　　●●●○●●○○○○
LV 7=　　　　　　　　　　　　　　　●○○●●●●●　　　○○○○
LV 8=　　　　　　　　　　　　　　　　　　●●●●●●○○○○○○

解説

反復深化深さ優先探索と下限値枝切りを組み合わせてます。

下限値枝切りでの必要な最低手数の算出ロジックとして、
例えば、下記のような石の配置の場合は、
解に到達するのに、最低でもあと2手かかります。
連続してない白石が3つあるので、白石を連続させるためには、最低2手必要で、
連続してない黒石が2つあるので、黒石を連続させるためには、最低1手必要で、
白石と黒石で必要手数の多いほうは、2手だからです。

○●○●○

8-22 おしどりの遊び1 石が5個