Cマガ電脳クラブ(第046回) ダブル小町虫食い算

問題

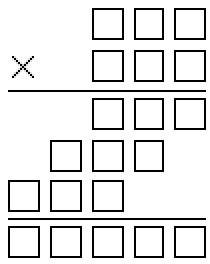
今回は虫食い算の問題だ。Fig.1の□の中に数字を入れて、正しい式として完成すればよい。
だがもう一つ条件がある。それは 0, 1, 2, … 9 の10個の数字を、すべてそれぞれ2回ずつ使うというものだ。
各数の左端は0ではない。当然、□は20個ある。
おそらく紙とエンピツだけで解いてしまう人もいるだろう。

Fig.1 ダブル小町虫食い算

ソース

using System;
using System.Collections.Generic;

class Program
{
    static void Main()
    {
        for (int I = 100; I <= 999; I++) {
            for (int J = I; J <= 999; J++) {
                if (DeriveKetasuu(I * J) <= 4) continue;
                CheckEachCombi(I, J);
                if (DeriveKetasuu(I * J) >= 6) break;
            }
        }
    }

    //各組み合わせをチェック
    static void CheckEachCombi(int pI, int pJ)
    {
        int ProdOfKeta1 = (pJ % 10) * pI;
        int ProdOfKeta10 = (pJ / 10 % 10) * pI;
        int ProdOfKeta100 = (pJ / 100) * pI;
        int ProdVal = pI * pJ;

        if (DeriveKetasuu(ProdOfKeta1) != 3) return;
        if (DeriveKetasuu(ProdOfKeta10) != 3) return;
        if (DeriveKetasuu(ProdOfKeta100) != 3) return;

        var wkList = new List<int>();
        wkList.Add(pI);
        wkList.Add(pJ);
        wkList.Add(ProdOfKeta1);
        wkList.Add(ProdOfKeta10);
        wkList.Add(ProdOfKeta100);
        wkList.Add(ProdVal);
        if (IsValidVals(wkList) == false) return;
        Console.WriteLine("{0}*{1}を解として発見", pI, pJ);
        PrintAnswer(wkList);
    }

    //数値の桁数を返す
    static int DeriveKetasuu(int pTarget)
    {
        if (pTarget < 10) return 1;
        if (pTarget < 100) return 2;
        if (pTarget < 1000) return 3;
        if (pTarget < 10000) return 4;
        if (pTarget < 100000) return 5;
        return 6;
    }

    //有効な数値リストかを判定
    static bool IsValidVals(List<int> pValList)
    {
        int[] AppearedCntArr = new int[10];

        foreach (int AnyInt in pValList) {
            int CopiedVal = AnyInt;
            do {
                int ModVal = CopiedVal % 10;

                //同じ数字を3個以上含んだらNG
                if (AppearedCntArr[ModVal] >= 2) return false;
                AppearedCntArr[ModVal]++;
            } while ((CopiedVal /= 10) > 0);
        }
        return true;
    }

    //解を筆算の形で表示
    static void PrintAnswer(List<int> pValList)
    {
        Console.WriteLine("  {0}", pValList[0]);
        Console.WriteLine(" *{0}", pValList[1]);
        Console.WriteLine("-----");
        Console.WriteLine("  {0}", pValList[2]);
        Console.WriteLine(" {0}", pValList[3]);
        Console.WriteLine(pValList[4]);
        Console.WriteLine("-----");
        Console.WriteLine(pValList[5]);
    }
}

実行結果

179*224を解として発見
  179
 *224
-----
  716
 358
358
-----
40096

解説

For文で掛け算の組み合わせを列挙して、
順にチェックしてます。