using System;
using System.Collections.Generic;
using System.Linq;
class Program
{
static int UB;
struct JyoutaiDef
{
internal int Level;
internal int[,] BanArr;
}
//各面の状態を表す変数
//状態1 状態2 状態3 状態4 状態9
//* *** *** * ***
//** ** ** ** ***
//*** * * *** ***
static System.Diagnostics.Stopwatch sw = System.Diagnostics.Stopwatch.StartNew();
static void Main()
{
for (int Depth = 1; Depth <= 10; Depth++) {
Console.WriteLine("基本形の数={0}で解を検証中。", Depth);
int NeedLength = 0; //ポリアボロの最大の幅
if (Depth == 1) NeedLength = 1;
if (Depth == 2) NeedLength = 2;
if (Depth == 3) NeedLength = 2;
if (Depth == 4) NeedLength = 3;
if (Depth == 5) NeedLength = 3;
if (Depth == 6) NeedLength = 4;
if (Depth == 7) NeedLength = 4;
if (Depth == 8) NeedLength = 5;
if (Depth == 9) NeedLength = 5;
if (Depth == 10) NeedLength = 6;
UB = NeedLength * 2; //2次元配列の中央から三角形を配置する
ExecDFS(Depth);
}
}
//中間ノードの定義
struct TyuukanNodeDef
{
internal int Level;
internal int[,] BanArr;
internal int SquareCnt;
}
//深さ制限を引数として深さ優先探索を行う
static void ExecDFS(int pDepthMax)
{
var stk = new Stack<JyoutaiDef>();
JyoutaiDef WillPush;
WillPush.Level = 1;
WillPush.BanArr = new int[UB + 1, UB + 1];
WillPush.BanArr[UB / 2, UB / 2] = 1; //回転解の除外で1個目の三角形は回転させない
stk.Push(WillPush);
var AnswerBanList = new List<int[,]>();
//中間ノードのリスト
var TyuukanNodeList = new List<TyuukanNodeDef>();
while (stk.Count > 0) {
JyoutaiDef Popped = stk.Pop();
//2次元配列の縮小(X軸方向とY軸方向の空白マスを削除)
int[,] ReducedArr = ExecReduceArr(Popped.BanArr);
TyuukanNodeDef TyuukanNode;
TyuukanNode.Level = Popped.Level;
TyuukanNode.BanArr = ReducedArr;
TyuukanNode.SquareCnt = DeriveSquareCnt(ReducedArr);
//遷移済状態なら枝切り
if (IsDuplicateJyoutai(TyuukanNodeList, TyuukanNode)) continue;
TyuukanNodeList.Add(TyuukanNode);
//クリア判定
if (Popped.Level == pDepthMax) {
AnswerBanList.Add(ReducedArr);
continue;
}
//候補のポリアボロのListを返す
List<int[,]> KouhoPolyaboloList = DeriveKouhoPolyaboloList(Popped.BanArr);
foreach (int[,] EachBanArr in KouhoPolyaboloList) {
WillPush.Level = Popped.Level + 1;
WillPush.BanArr = EachBanArr;
stk.Push(WillPush);
}
}
Console.WriteLine("解は{0,5}通り。経過時間={1}",
AnswerBanList.Count, sw.Elapsed);
//for (int I = 0; I <= AnswerBanList.Count - 1; I++) {
// Console.WriteLine("解{0}。経過時間={1}", I + 1, sw.Elapsed);
// PrintAnswer(AnswerBanList[I]);
//}
}
//2次元配列の縮小(X軸方向とY軸方向の空白マスを削除)
static int[,] ExecReduceArr(int[,] pBanArr)
{
int[,] WillReturnArr;
int XMin = pBanArr.GetUpperBound(0), YMin = pBanArr.GetUpperBound(1);
int XMax = 0, YMax = 0;
for (int X = 0; X <= pBanArr.GetUpperBound(0); X++) {
for (int Y = 0; Y <= pBanArr.GetUpperBound(1); Y++) {
if (pBanArr[X, Y] == 0) continue;
if (XMin > X) XMin = X;
if (YMin > Y) YMin = Y;
if (XMax < X) XMax = X;
if (YMax < Y) YMax = Y;
}
}
WillReturnArr = new int[XMax - XMin + 1, YMax - YMin + 1];
for (int X = 0; X <= WillReturnArr.GetUpperBound(0); X++) {
for (int Y = 0; Y <= WillReturnArr.GetUpperBound(1); Y++) {
WillReturnArr[X, Y] = pBanArr[XMin + X, YMin + Y];
}
}
return WillReturnArr;
}
//盤面の正方形の数を返す
static int DeriveSquareCnt(int[,] pBanArr)
{
int WillReturn = 0;
for (int X = 0; X <= pBanArr.GetUpperBound(0); X++) {
for (int Y = 0; Y <= pBanArr.GetUpperBound(1); Y++) {
if (pBanArr[X, Y] == 9) WillReturn++;
}
}
return WillReturn;
}
//重複した状態かのチェック
static bool IsDuplicateJyoutai(List<TyuukanNodeDef> pTyuukanNodeList, TyuukanNodeDef pTyuukanNode)
{
foreach (TyuukanNodeDef EachTyuukanNode in pTyuukanNodeList) {
if (EachTyuukanNode.Level != pTyuukanNode.Level) continue;
if (EachTyuukanNode.SquareCnt != pTyuukanNode.SquareCnt) continue;
int[,] wkArr;
//1 そのまま
wkArr = EachTyuukanNode.BanArr;
if (IsEqualArr(wkArr, pTyuukanNode.BanArr)) return true;
//2 右に90度回転
wkArr = Kaiten90do(wkArr);
if (IsEqualArr(wkArr, pTyuukanNode.BanArr)) return true;
//3 右に180度回転
wkArr = Kaiten90do(wkArr);
if (IsEqualArr(wkArr, pTyuukanNode.BanArr)) return true;
//4 右に270度回転
wkArr = Kaiten90do(wkArr);
if (IsEqualArr(wkArr, pTyuukanNode.BanArr)) return true;
//5 左右反転
wkArr = SayuuHanten(wkArr);
if (IsEqualArr(wkArr, pTyuukanNode.BanArr)) return true;
//6 右に90度回転
wkArr = Kaiten90do(wkArr);
if (IsEqualArr(wkArr, pTyuukanNode.BanArr)) return true;
//7 右に180度回転
wkArr = Kaiten90do(wkArr);
if (IsEqualArr(wkArr, pTyuukanNode.BanArr)) return true;
//8 右に270度回転
wkArr = Kaiten90do(wkArr);
if (IsEqualArr(wkArr, pTyuukanNode.BanArr)) return true;
}
return false;
}
//2次元配列同士が、同じ要素数で同じ中身かを返す
static bool IsEqualArr(int[,] pBanArr1, int[,] pBanArr2)
{
int Arr1_UB_X = pBanArr1.GetUpperBound(0);
int Arr1_UB_Y = pBanArr1.GetUpperBound(1);
int Arr2_UB_X = pBanArr2.GetUpperBound(0);
int Arr2_UB_Y = pBanArr2.GetUpperBound(1);
//X軸の要素数チェック
if (Arr1_UB_X != Arr2_UB_X) return false;
//Y軸の要素数チェック
if (Arr1_UB_Y != Arr2_UB_Y) return false;
for (int X = 0; X <= Arr1_UB_X; X++)
for (int Y = 0; Y <= Arr1_UB_Y; Y++)
if (pBanArr1[X, Y] != pBanArr2[X, Y])
return false;
return true;
}
//右に90度回転させた盤面を返す
static int[,] Kaiten90do(int[,] pBanArr)
{
int[,] WillReturn = new int[pBanArr.GetUpperBound(1) + 1,
pBanArr.GetUpperBound(0) + 1];
for (int X = 0; X <= WillReturn.GetUpperBound(0); X++) {
for (int Y = 0; Y <= WillReturn.GetUpperBound(1); Y++) {
int wkVal = pBanArr[Y, WillReturn.GetUpperBound(0) - X];
//各面の三角形も90度回転させる
switch (wkVal) {
case 1: wkVal = 2; break;
case 2: wkVal = 3; break;
case 3: wkVal = 4; break;
case 4: wkVal = 1; break;
}
WillReturn[X, Y] = wkVal;
}
}
return WillReturn;
}
//左右反転させた盤面を返す
static int[,] SayuuHanten(int[,] pBanArr)
{
int[,] WillReturn = new int[pBanArr.GetUpperBound(0) + 1,
pBanArr.GetUpperBound(1) + 1];
for (int X = 0; X <= WillReturn.GetUpperBound(0); X++) {
for (int Y = 0; Y <= WillReturn.GetUpperBound(1); Y++) {
int wkVal = pBanArr[WillReturn.GetUpperBound(0) - X, Y];
//各面の三角形も左右反転させる
switch (wkVal) {
case 1: wkVal = 4; break;
case 2: wkVal = 3; break;
case 3: wkVal = 2; break;
case 4: wkVal = 1; break;
}
WillReturn[X, Y] = wkVal;
}
}
return WillReturn;
}
//候補のポリアボロのListを返す
static List<int[,]> DeriveKouhoPolyaboloList(int[,] pBanArr)
{
var WillReturnList = new List<int[,]>();
Action<int, int, int> wkACT = (pX, pY, pKind) =>
{
int[,] WKbanArr;
if (CanAddSankakukei(pX, pY, pKind, pBanArr, out WKbanArr))
WillReturnList.Add(WKbanArr);
};
for (int X = 0; X <= UB; X++) {
for (int Y = 0; Y <= UB; Y++) {
if (pBanArr[X, Y] == 0) continue;
if (pBanArr[X, Y] == 1) {
wkACT(X - 1, Y, 3); wkACT(X - 1, Y, 4);
wkACT(X, Y + 1, 2); wkACT(X, Y + 1, 3);
wkACT(X, Y, 3);
}
if (pBanArr[X, Y] == 2) {
wkACT(X - 1, Y, 3); wkACT(X - 1, Y, 4);
wkACT(X, Y - 1, 1); wkACT(X, Y - 1, 4);
wkACT(X, Y, 4);
}
if (pBanArr[X, Y] == 3) {
wkACT(X, Y - 1, 1); wkACT(X, Y - 1, 4);
wkACT(X + 1, Y, 1); wkACT(X + 1, Y, 2);
wkACT(X, Y, 1);
}
if (pBanArr[X, Y] == 4) {
wkACT(X, Y + 1, 2); wkACT(X, Y + 1, 3);
wkACT(X + 1, Y, 1); wkACT(X + 1, Y, 2);
wkACT(X, Y, 2);
}
if (pBanArr[X, Y] == 9) {
wkACT(X - 1, Y, 3); wkACT(X - 1, Y, 4);
wkACT(X, Y - 1, 1); wkACT(X, Y - 1, 4);
wkACT(X + 1, Y, 1); wkACT(X + 1, Y, 2);
wkACT(X, Y + 1, 2); wkACT(X, Y + 1, 3);
}
}
}
return WillReturnList;
}
//追加先座標、追加三角形の種類、現在の盤面、三角形追加後の盤面
//を引数として、三角形を追加できるかを返す
static bool CanAddSankakukei(int pX, int pY, int pAddKind, int[,] pBanArr, out int[,] pWKbanArr)
{
pWKbanArr = null;
int CurrKind = pBanArr[pX, pY];
bool CanAdd = false;
if (pAddKind == 1) CanAdd = (CurrKind == 0 || CurrKind == 3);
if (pAddKind == 2) CanAdd = (CurrKind == 0 || CurrKind == 4);
if (pAddKind == 3) CanAdd = (CurrKind == 0 || CurrKind == 1);
if (pAddKind == 4) CanAdd = (CurrKind == 0 || CurrKind == 2);
if (CanAdd == false) return false;
pWKbanArr = (int[,])pBanArr.Clone();
if (pAddKind == 1) pWKbanArr[pX, pY] = (CurrKind == 0 ? 1 : 9);
if (pAddKind == 2) pWKbanArr[pX, pY] = (CurrKind == 0 ? 2 : 9);
if (pAddKind == 3) pWKbanArr[pX, pY] = (CurrKind == 0 ? 3 : 9);
if (pAddKind == 4) pWKbanArr[pX, pY] = (CurrKind == 0 ? 4 : 9);
return true;
}
//解を出力
static void PrintAnswer(int[,] pBanArr)
{
var sb = new System.Text.StringBuilder();
for (int Y = 0; Y <= pBanArr.GetUpperBound(1); Y++) {
for (int X = 0; X <= pBanArr.GetUpperBound(0); X++) {
if (pBanArr[X, Y] == 0) sb.Append('*');
else sb.Append(pBanArr[X, Y]);
}
sb.AppendLine();
}
Console.WriteLine(sb.ToString());
}
}
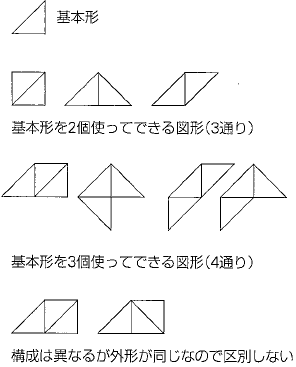
Fig.A ポリアボロ