Cマガ電脳クラブ(第074回) ノナ

問題

正12面体の面に12枚のタイルを貼り付けるドデカパズルというシリーズに、かつて「ノナ」という名の名作があった。

まずFig.1を見ていただきたい。
12枚の正5角形のタイルがあり、それぞれの5つの角には1〜5の数字が書いてある。
各タイルの数字の並び方をよく見ると、すべて異なっている。

各数字の裏にはそれぞれ同じ数字が書かれており、
たとえば(a)のタイルを時計回りに読むと1,2,3,4,5だが、
裏は同様に時計回りで読むと1,5,4,3,2となっている(Fig.2)。

さて、ここで各面がタイルと同じ大きさの正12面体(Fig.3)を用意し、
12枚のタイルをこの面に貼り付けてみる。
このときこの立体の20個の頂点に注目すると、
その周りに3枚のタイルの角がくるので、3つの数字で囲まれることになる。

では、この3つの数の合計がどの頂点でも9になる貼り付け方は何通りあるか。
もちろん、回転・鏡像解は別解とはしない。


     

ノナの紹介画像

ソース

using System;
using System.Collections.Generic;
using System.Linq;

class Program
{
    //タイルごとの配置候補
    static Dictionary<char, List<int[]>> HaitiKouhoListDict =
        new Dictionary<char, List<int[]>>();

    struct JyoutaiDef
    {
        internal int MenCnt;
        internal List<TileInfoDef> TileInfoList;
    }

    //設置したタイルの情報
    struct TileInfoDef
    {
        internal char TileID; //タイルID (aからj)
        internal int MenNo; //面番号 (1から12)
        internal int TyoutenNo; //頂点番号 (1から5)
        internal int TyoutenVal; //その頂点の値 (1から5)
    }

    static void Main()
    {
        var sw = System.Diagnostics.Stopwatch.StartNew();

        for (char I = 'a'; I <= 'l'; I++) {
            HaitiKouhoListDict[I] = DeriveHaitiKouhoListDict(I);
        }
        //回転解の除外で、aは回転させない
        HaitiKouhoListDict['a'].RemoveRange(1, HaitiKouhoListDict['a'].Count - 1);

        //設置した面の頂点情報をAdd
        Action<List<TileInfoDef>, char, int, int[]> AddTileInfoAct =
            (pTileInfoList, pTileID, pMenNo, pHaitiArr) =>
            {
                TileInfoDef WillAdd;
                WillAdd.TileID = pTileID;
                WillAdd.MenNo = pMenNo;
                for (int I = 0; I <= pHaitiArr.GetUpperBound(0); I++) {
                    WillAdd.TyoutenNo = I;
                    WillAdd.TyoutenVal = pHaitiArr[I];
                    pTileInfoList.Add(WillAdd);
                }
            };

        var stk = new Stack<JyoutaiDef>();
        JyoutaiDef WillPush;

        //回転解の除外で、1枚目はaとする
        WillPush.MenCnt = 1;
        WillPush.TileInfoList = new List<TileInfoDef>();
        AddTileInfoAct(WillPush.TileInfoList, 'a', 1, HaitiKouhoListDict['a'][0]);
        stk.Push(WillPush);

        int AnswerCnt = 0;

        while (stk.Count > 0) {
            JyoutaiDef Popped = stk.Pop();

            //クリア判定
            if (Popped.MenCnt == 12) {
                Console.WriteLine("解{0}を発見。経過時間={1}", ++AnswerCnt, sw.Elapsed);
                PrintAnswer(Popped.TileInfoList);
                continue;
            }

            foreach (var EachPair in HaitiKouhoListDict) {
                if (Popped.TileInfoList.Exists(X => X.TileID == EachPair.Key)) continue;

                WillPush.MenCnt = Popped.MenCnt + 1;
                foreach (int[] EachArr in EachPair.Value) {
                    WillPush.TileInfoList = new List<TileInfoDef>(Popped.TileInfoList);
                    AddTileInfoAct(WillPush.TileInfoList, EachPair.Key, WillPush.MenCnt, EachArr);

                    if (WillEdakiri(WillPush.MenCnt, WillPush.TileInfoList) == false)
                        stk.Push(WillPush);
                }
            }
        }
    }

    //枝切り判定
    static bool WillEdakiri(int pMenCnt, List<TileInfoDef> pTileInfoList)
    {
        if (WillEdakiriHelper(pMenCnt, pTileInfoList, 1, 0, 5, 0, 9, 0)) return true;
        if (WillEdakiriHelper(pMenCnt, pTileInfoList, 1, 1, 3, 0, 5, 4)) return true;
        if (WillEdakiriHelper(pMenCnt, pTileInfoList, 1, 2, 2, 0, 3, 4)) return true;
        if (WillEdakiriHelper(pMenCnt, pTileInfoList, 1, 3, 2, 4, 11, 1)) return true;
        if (WillEdakiriHelper(pMenCnt, pTileInfoList, 1, 4, 9, 1, 11, 0)) return true;
        if (WillEdakiriHelper(pMenCnt, pTileInfoList, 2, 1, 3, 3, 4, 4)) return true;
        if (WillEdakiriHelper(pMenCnt, pTileInfoList, 2, 2, 4, 3, 12, 1)) return true;
        if (WillEdakiriHelper(pMenCnt, pTileInfoList, 2, 3, 11, 2, 12, 0)) return true;
        if (WillEdakiriHelper(pMenCnt, pTileInfoList, 3, 1, 5, 3, 6, 4)) return true;
        if (WillEdakiriHelper(pMenCnt, pTileInfoList, 3, 2, 4, 0, 6, 3)) return true;
        if (WillEdakiriHelper(pMenCnt, pTileInfoList, 4, 1, 6, 2, 8, 3)) return true;
        if (WillEdakiriHelper(pMenCnt, pTileInfoList, 4, 2, 8, 2, 12, 2)) return true;
        if (WillEdakiriHelper(pMenCnt, pTileInfoList, 5, 1, 7, 0, 9, 4)) return true;
        if (WillEdakiriHelper(pMenCnt, pTileInfoList, 5, 2, 6, 0, 7, 4)) return true;
        if (WillEdakiriHelper(pMenCnt, pTileInfoList, 6, 1, 7, 3, 8, 4)) return true;
        if (WillEdakiriHelper(pMenCnt, pTileInfoList, 7, 1, 9, 3, 10, 4)) return true;
        if (WillEdakiriHelper(pMenCnt, pTileInfoList, 7, 2, 8, 0, 10, 3)) return true;
        if (WillEdakiriHelper(pMenCnt, pTileInfoList, 8, 1, 10, 2, 12, 3)) return true;
        if (WillEdakiriHelper(pMenCnt, pTileInfoList, 9, 2, 10, 0, 11, 4)) return true;
        if (WillEdakiriHelper(pMenCnt, pTileInfoList, 10, 1, 11, 3, 12, 4)) return true;
        return false;
    }

    //枝切り判定のヘルパメソッド
    static bool WillEdakiriHelper(int pMenCnt, List<TileInfoDef> pTileInfoList,
        int pMen1, int pTyouten1, int pMen2, int pTyouten2, int pMen3, int pTyouten3)
    {
        //設置した面を含む枝切り条件のみ判定
        if (pMenCnt != pMen1 && pMenCnt != pMen2 && pMenCnt != pMen3) return false;

        int SumVal = 0;
        int Cnt = 0;

        Action<int, int> wkAct = (pMen, pTyouten) =>
        {
            int wkInd = pTileInfoList.FindIndex(X => X.MenNo == pMen
                                                  && X.TyoutenNo == pTyouten);
            if (wkInd >= 0) {
                SumVal += pTileInfoList[wkInd].TyoutenVal;
                Cnt++;
            }
        };
        wkAct(pMen1, pTyouten1);
        wkAct(pMen2, pTyouten2);
        wkAct(pMen3, pTyouten3);
        if (Cnt == 3) return SumVal != 9;
        if (Cnt == 2 && SumVal >= 9) return true;
        if (Cnt == 2 && SumVal <= 3) return true;
        return false;
    }

    //タイル名を引数として、回転させた配置のListを返す
    static List<int[]> DeriveHaitiKouhoListDict(char pTileName)
    {
        int[] wkArr = null;
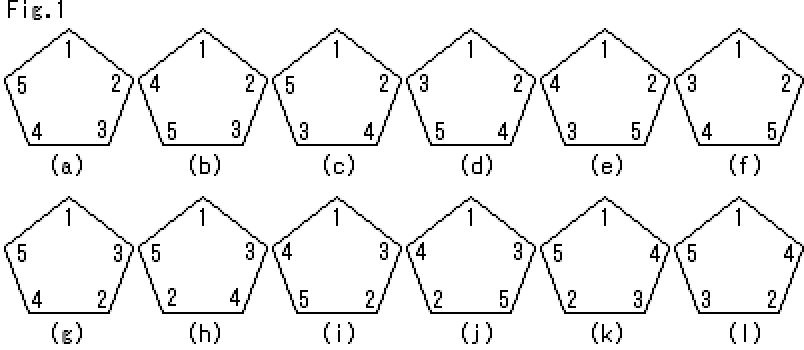
        if (pTileName == 'a') wkArr = new int[] { 1, 2, 3, 4, 5 };
        if (pTileName == 'b') wkArr = new int[] { 1, 2, 3, 5, 4 };
        if (pTileName == 'c') wkArr = new int[] { 1, 2, 4, 3, 5 };
        if (pTileName == 'd') wkArr = new int[] { 1, 2, 4, 5, 3 };
        if (pTileName == 'e') wkArr = new int[] { 1, 2, 5, 3, 4 };
        if (pTileName == 'f') wkArr = new int[] { 1, 2, 5, 4, 3 };
        if (pTileName == 'g') wkArr = new int[] { 1, 3, 2, 4, 5 };
        if (pTileName == 'h') wkArr = new int[] { 1, 3, 4, 2, 5 };
        if (pTileName == 'i') wkArr = new int[] { 1, 3, 2, 5, 4 };
        if (pTileName == 'j') wkArr = new int[] { 1, 3, 5, 2, 4 };
        if (pTileName == 'k') wkArr = new int[] { 1, 4, 3, 2, 5 };
        if (pTileName == 'l') wkArr = new int[] { 1, 4, 2, 3, 5 };

        return DeriveKaitenArrList(wkArr);
    }

    //配列を引数として、回転させた配列のリストを返す
    static List<int[]> DeriveKaitenArrList(int[] pBaseArr)
    {
        var WillReturn = new List<int[]>();
        WillReturn.Add(DeriveKaitenArrListHelper(pBaseArr, 0, 1, 2, 3, 4));
        WillReturn.Add(DeriveKaitenArrListHelper(pBaseArr, 1, 2, 3, 4, 0));
        WillReturn.Add(DeriveKaitenArrListHelper(pBaseArr, 2, 3, 4, 0, 1));
        WillReturn.Add(DeriveKaitenArrListHelper(pBaseArr, 3, 4, 0, 1, 2));
        WillReturn.Add(DeriveKaitenArrListHelper(pBaseArr, 4, 0, 1, 2, 3));

        WillReturn.Add(DeriveKaitenArrListHelper(pBaseArr, 4, 3, 2, 1, 0));
        WillReturn.Add(DeriveKaitenArrListHelper(pBaseArr, 3, 2, 1, 0, 4));
        WillReturn.Add(DeriveKaitenArrListHelper(pBaseArr, 2, 1, 0, 4, 3));
        WillReturn.Add(DeriveKaitenArrListHelper(pBaseArr, 1, 0, 4, 3, 2));
        WillReturn.Add(DeriveKaitenArrListHelper(pBaseArr, 0, 4, 3, 2, 1));

        return WillReturn;
    }

    //配列を引数として、回転させた配列のリストを返す
    static int[] DeriveKaitenArrListHelper(int[] pBaseArr, int p0, int p1, int p2, int p3, int p4)
    {
        return new int[] { pBaseArr[p0], pBaseArr[p1], pBaseArr[p2], pBaseArr[p3], pBaseArr[p4] };
    }

    //解を出力
    static void PrintAnswer(List<TileInfoDef> pTileInfoList)
    {
        var sb = new System.Text.StringBuilder();
        var Tmp = pTileInfoList.OrderBy(X => X.MenNo).ThenBy(X => X.TyoutenNo);
        int OutCnt = 0;
        foreach (TileInfoDef EachTileInfo in Tmp) {
            if (OutCnt == 0) {
                sb.AppendFormat("使用タイル={0},", EachTileInfo.TileID);
                sb.AppendFormat("面番号={0,2},", EachTileInfo.MenNo);
            }
            sb.AppendFormat("頂点{0}={1},", EachTileInfo.TyoutenNo, EachTileInfo.TyoutenVal);

            if (++OutCnt == 5) {
                OutCnt = 0;
                sb.AppendLine();
            }
        }
        Console.WriteLine(sb.ToString());
    }
}

実行結果

省略
解1122を発見。経過時間=00:12:28.7272382
使用タイル=a,面番号= 1,頂点0=1,頂点1=2,頂点2=3,頂点3=4,頂点4=5,
使用タイル=b,面番号= 2,頂点0=1,頂点1=2,頂点2=3,頂点3=5,頂点4=4,
使用タイル=i,面番号= 3,頂点0=2,頂点1=3,頂点2=1,頂点3=4,頂点4=5,
使用タイル=j,面番号= 4,頂点0=5,頂点1=2,頂点2=4,頂点3=1,頂点4=3,
使用タイル=d,面番号= 5,頂点0=3,頂点1=1,頂点2=2,頂点3=4,頂点4=5,
使用タイル=l,面番号= 6,頂点0=4,頂点1=1,頂点2=5,頂点3=3,頂点4=2,
使用タイル=c,面番号= 7,頂点0=5,頂点1=1,頂点2=2,頂点3=4,頂点4=3,
使用タイル=g,面番号= 8,頂点0=5,頂点1=1,頂点2=3,頂点3=2,頂点4=4,
使用タイル=e,面番号= 9,頂点0=5,頂点1=2,頂点2=1,頂点3=4,頂点4=3,
使用タイル=h,面番号=10,頂点0=3,頂点1=1,頂点2=5,頂点3=2,頂点4=4,
使用タイル=f,面番号=11,頂点0=2,頂点1=1,頂点2=3,頂点3=4,頂点4=5,
使用タイル=k,面番号=12,頂点0=1,頂点1=5,頂点2=2,頂点3=3,頂点4=4,

解説

正12面体の展開図の
各面に、数値を割り当て、
各頂点に、アルファベットのAからTを割り当てると、下記となります。



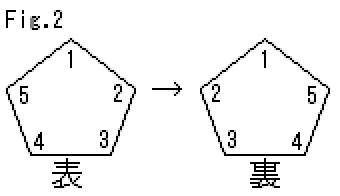
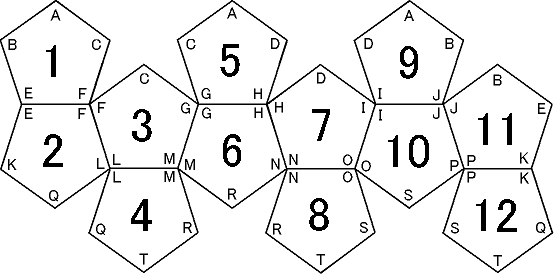頂点番号は、正5角形の
(A,C,F,E,B)に(0,1,2,3,4)、および
(F,L,Q,K,E)に(0,1,2,3,4)という順序で振ってます。

そして、深さ優先探索で全探索してます。
頂点の2つの数が確定した時点で
3以下の場合と9以上の場合を枝切りしてます。

Cマガ電脳クラブ(第087回) 正12面体魔方陣