トップページに戻る    次のC#のサンプルへ    前のC#のサンプルへ

Cマガ電脳クラブ(第079回) Planar Pentacubes

問題

1辺の長さが1の正方形のタイル5個を、
辺同士でくっつけて組み合わせたものをペントミノといい、全12種類の型がある。

このペントミノは、それぞれの形からアルファベットの名前が付いている(Fig.A)。
一方、1辺の長さが1の立方体5個を面同士でくっつけて組み合わせたものをペンタキューブといい、
全部で29種類ある。

さて、ペントミノのタイルを立方体で置き換えたペンタキューブ8つまり厚さが1のペントミノ)を
特別にプラナーペンタキューブという。

この12種類のプラナーペンタキューブを全て使って、
底面の形状がPペントミノで高さが12の立体(Fig.B)に組み上げたい。何通りの組み方があるか

ソース

using System;
using System.Collections.Generic;
using System.Linq;

class Program
{
    //ピースごとの配置候補
    static Dictionary<char, List<bool[, ,]>> HaitiKouhoListDict =
        new Dictionary<char, List<bool[, ,]>>();

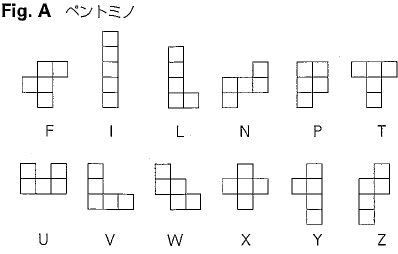
    static char[] PieceNameArr = { 'F', 'I', 'L', 'N', 'P', 'T',
                                   'U', 'V', 'W', 'X', 'Y', 'Z'};

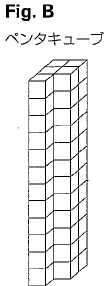
    const int UB_X = 2 - 1;
    const int UB_Y = 3 - 1;
    const int UB_Z = 12 - 1;

    struct JyoutaiDef
    {
        internal char[, ,] BanArr;
        internal int CurrX;
        internal int CurrY;
        internal int CurrZ;
        internal int PentominoCnt;
    }

    static void Main()
    {
        var sw = System.Diagnostics.Stopwatch.StartNew();

        foreach (char AnyPiece in PieceNameArr) {
            HaitiKouhoListDict[AnyPiece] = DeriveHaitiKouhoList(AnyPiece);
        }

        //UB超えの回転をRemove
        foreach (var EachPair in HaitiKouhoListDict) {
            EachPair.Value.RemoveAll(A => A.GetUpperBound(0) > UB_X
                                       || A.GetUpperBound(1) > UB_Y);
        }

        var stk = new Stack<JyoutaiDef>();
        JyoutaiDef WillPush;
        WillPush.BanArr = new char[UB_X + 1, UB_Y + 1, UB_Z + 1];
        for (int X = 0; X <= UB_X; X++)
            for (int Y = 0; Y <= UB_Y; Y++)
                for (int Z = 0; Z <= UB_Z; Z++)
                    WillPush.BanArr[X, Y, Z] = ' ';
        for (int Z = 0; Z <= UB_Z; Z++)
            WillPush.BanArr[UB_X, UB_Y, Z] = '*';

        WillPush.CurrX = WillPush.CurrY = WillPush.CurrZ = 0;
        WillPush.PentominoCnt = 0;
        stk.Push(WillPush);

        int AnwserCnt = 0;

        while (stk.Count > 0) {
            JyoutaiDef Popped = stk.Pop();

            //クリア判定
            if (Popped.PentominoCnt == 12) {
                Console.WriteLine("解{0}を発見。経過時間={1}", ++AnwserCnt, sw.Elapsed);
                PrintAnswer(Popped.BanArr);
                return;
            }

            //X座標の繰上げ処理
            if (Popped.CurrX > UB_X) {
                Popped.CurrX = 0;
                Popped.CurrY++;
            }

            //最終行を超えた場合
            if (Popped.CurrY > UB_Y) {
                Popped.CurrY = 0;

                //最終高さを超えた場合
                if (++Popped.CurrZ > UB_Z) continue;
            }

            //使用済のピース名の配列
            char[] UsedPieceArr = Popped.BanArr.Cast<char>().Distinct().ToArray();

            //回転解の除外で、Iペンタキューブは、Yが5以下の座標から配置する
            if (Array.IndexOf(UsedPieceArr, 'I') < 0 && Popped.CurrY > 5) continue;

            foreach (char AnyPiece in PieceNameArr) {
                if (Array.IndexOf(UsedPieceArr, AnyPiece) >= 0) continue;

                //ピースの配置候補リスト
                List<bool[, ,]> HaitiKouhoList = new List<bool[, ,]>();
                HaitiKouhoList.AddRange(HaitiKouhoListDict[AnyPiece]);

                //現在のマス目が空白の場合は、マス目を埋める必要あり
                if (Popped.BanArr[Popped.CurrX, Popped.CurrY, Popped.CurrZ] == ' ') {
                    HaitiKouhoList.RemoveAll(X => X[0, 0, 0] == false);
                }

                //マス目にピースを埋めれない候補をRemove
                HaitiKouhoList.RemoveAll(X =>
                    CanFillPiece(X, Popped.CurrX, Popped.CurrY, Popped.CurrZ, Popped.BanArr) == false);

                //ピースを配置する経路のPush処理
                foreach (bool[, ,] AnyPieceMap in HaitiKouhoList) {
                    WillPush.BanArr = (char[, ,])Popped.BanArr.Clone();
                    WillPush.CurrX = Popped.CurrX;
                    WillPush.CurrY = Popped.CurrY;
                    WillPush.CurrZ = Popped.CurrZ;
                    WillPush.PentominoCnt = Popped.PentominoCnt + 1;

                    for (int X = 0; X <= AnyPieceMap.GetUpperBound(0); X++) {
                        for (int Y = 0; Y <= AnyPieceMap.GetUpperBound(1); Y++) {
                            for (int Z = 0; Z <= AnyPieceMap.GetUpperBound(2); Z++) {
                                if (AnyPieceMap[X, Y, Z] == false) continue;
                                WillPush.BanArr[Popped.CurrX + X, Popped.CurrY + Y, Popped.CurrZ + Z]
                                    = AnyPiece;
                            }
                        }
                    }
                    stk.Push(WillPush);
                }
            }

            //現在のマス目が空白でない場合は、ピースを配置しない経路のPush
            if (Popped.BanArr[Popped.CurrX, Popped.CurrY, Popped.CurrZ] != ' ') {
                WillPush.BanArr = Popped.BanArr;
                WillPush.CurrX = Popped.CurrX + 1;
                WillPush.CurrY = Popped.CurrY;
                WillPush.CurrZ = Popped.CurrZ;
                WillPush.PentominoCnt = Popped.PentominoCnt;
                stk.Push(WillPush);
            }
        }
    }

    //ピース名を引数として、回転させた配置のListを返す
    static List<bool[, ,]> DeriveHaitiKouhoList(char pPieceName)
    {
        bool[, ,] wkArr = null;

        //　■■
        //■■
        //　■
        if (pPieceName == 'F') {
            wkArr = new bool[3, 3, 1];
            wkArr[0, 0, 0] = false; wkArr[1, 0, 0] = wkArr[2, 0, 0] = true;
            wkArr[0, 1, 0] = wkArr[1, 1, 0] = true; wkArr[2, 1, 0] = false;
            wkArr[0, 2, 0] = false; wkArr[1, 2, 0] = true; wkArr[2, 2, 0] = false;
        }

        //■
        //■
        //■
        //■
        //■
        if (pPieceName == 'I') {
            wkArr = new bool[1, 5, 1];
            wkArr[0, 0, 0] = wkArr[0, 1, 0] = wkArr[0, 2, 0] = wkArr[0, 3, 0] = wkArr[0, 4, 0] = true;
        }

        //■
        //■
        //■
        //■■
        if (pPieceName == 'L') {
            wkArr = new bool[2, 4, 1];
            wkArr[0, 0, 0] = true; wkArr[1, 0, 0] = false;
            wkArr[0, 1, 0] = true; wkArr[1, 1, 0] = false;
            wkArr[0, 2, 0] = true; wkArr[1, 2, 0] = false;
            wkArr[0, 3, 0] = wkArr[1, 3, 0] = true;
        }

        //　　■
        //■■■
        //■
        if (pPieceName == 'N') {
            wkArr = new bool[3, 3, 1];
            wkArr[0, 0, 0] = wkArr[1, 0, 0] = false; wkArr[2, 0, 0] = true;
            wkArr[0, 1, 0] = wkArr[1, 1, 0] = wkArr[2, 1, 0] = true;
            wkArr[0, 2, 0] = true; wkArr[1, 2, 0] = wkArr[2, 2, 0] = false;
        }

        //■■
        //■■
        //■
        if (pPieceName == 'P') {
            wkArr = new bool[2, 3, 1];
            wkArr[0, 0, 0] = wkArr[1, 0, 0] = true;
            wkArr[0, 1, 0] = wkArr[1, 1, 0] = true;
            wkArr[0, 2, 0] = true; wkArr[1, 2, 0] = false;
        }

        //■■■
        //　■
        //　■
        if (pPieceName == 'T') {
            wkArr = new bool[3, 3, 1];
            wkArr[0, 0, 0] = wkArr[1, 0, 0] = wkArr[2, 0, 0] = true;
            wkArr[0, 1, 0] = false; wkArr[1, 1, 0] = true; wkArr[2, 1, 0] = false;
            wkArr[0, 2, 0] = false; wkArr[1, 2, 0] = true; wkArr[2, 2, 0] = false;
        }

        //■　■
        //■■■
        if (pPieceName == 'U') {
            wkArr = new bool[3, 2, 1];
            wkArr[0, 0, 0] = true; wkArr[1, 0, 0] = false; wkArr[2, 0, 0] = true;
            wkArr[0, 1, 0] = wkArr[1, 1, 0] = wkArr[2, 1, 0] = true;
        }

        //■
        //■
        //■■■
        if (pPieceName == 'V') {
            wkArr = new bool[3, 3, 1];
            wkArr[0, 0, 0] = true; wkArr[1, 0, 0] = wkArr[2, 0, 0] = false;
            wkArr[0, 1, 0] = true; wkArr[1, 1, 0] = wkArr[2, 1, 0] = false;
            wkArr[0, 2, 0] = wkArr[1, 2, 0] = wkArr[2, 2, 0] = true;
        }

        //■
        //■■
        //　■■
        if (pPieceName == 'W') {
            wkArr = new bool[3, 3, 1];
            wkArr[0, 0, 0] = true; wkArr[1, 0, 0] = wkArr[2, 0, 0] = false;
            wkArr[0, 1, 0] = wkArr[1, 1, 0] = true; wkArr[2, 1, 0] = false;
            wkArr[0, 2, 0] = false; wkArr[1, 2, 0] = wkArr[2, 2, 0] = true;
        }

        //　■
        //■■■
        //　■
        if (pPieceName == 'X') {
            wkArr = new bool[3, 3, 1];
            wkArr[0, 0, 0] = false; wkArr[1, 0, 0] = true; wkArr[2, 0, 0] = false;
            wkArr[0, 1, 0] = wkArr[1, 1, 0] = wkArr[2, 1, 0] = true;
            wkArr[0, 2, 0] = false; wkArr[1, 2, 0] = true; wkArr[2, 2, 0] = false;
        }

        //　■
        //■■
        //　■
        //　■
        if (pPieceName == 'Y') {
            wkArr = new bool[2, 4, 1];
            wkArr[0, 0, 0] = false; wkArr[1, 0, 0] = true;
            wkArr[0, 1, 0] = wkArr[1, 1, 0] = true;
            wkArr[0, 2, 0] = false; wkArr[1, 2, 0] = true;
            wkArr[0, 3, 0] = false; wkArr[1, 3, 0] = true;
        }

        //　■
        //■■
        //■
        //■
        if (pPieceName == 'Z') {
            wkArr = new bool[2, 4, 1];
            wkArr[0, 0, 0] = false; wkArr[1, 0, 0] = true;
            wkArr[0, 1, 0] = wkArr[1, 1, 0] = true;
            wkArr[0, 2, 0] = true; wkArr[1, 2, 0] = false;
            wkArr[0, 3, 0] = true; wkArr[1, 3, 0] = false;
        }

        return DeriveKaitenArrList(wkArr);
    }

    //配列を引数として、回転させた配列のリストをDistinctして返す
    static List<bool[, ,]> DeriveKaitenArrList(bool[, ,] pBaseArr)
    {
        var KaitenArrList = new List<bool[, ,]>();

        int BaseUB_X = pBaseArr.GetUpperBound(0);
        int BaseUB_Y = pBaseArr.GetUpperBound(1);
        int BaseUB_Z = pBaseArr.GetUpperBound(2);

        for (int I = 1; I <= 48; I++) KaitenArrList.Add(null);
        for (int P = 0; P <= 7; P++) KaitenArrList[P] = new bool[BaseUB_X + 1, BaseUB_Y + 1, BaseUB_Z + 1];
        for (int P = 8; P <= 15; P++) KaitenArrList[P] = new bool[BaseUB_X + 1, BaseUB_Z + 1, BaseUB_Y + 1];
        for (int P = 16; P <= 23; P++) KaitenArrList[P] = new bool[BaseUB_Y + 1, BaseUB_X + 1, BaseUB_Z + 1];
        for (int P = 24; P <= 31; P++) KaitenArrList[P] = new bool[BaseUB_Y + 1, BaseUB_Z + 1, BaseUB_X + 1];
        for (int P = 32; P <= 39; P++) KaitenArrList[P] = new bool[BaseUB_Z + 1, BaseUB_X + 1, BaseUB_Y + 1];
        for (int P = 40; P <= 47; P++) KaitenArrList[P] = new bool[BaseUB_Z + 1, BaseUB_Y + 1, BaseUB_X + 1];

        for (int X = 0; X <= BaseUB_X; X++) {
            for (int Y = 0; Y <= BaseUB_Y; Y++) {
                for (int Z = 0; Z <= BaseUB_Z; Z++) {
                    bool SetVal = pBaseArr[X, Y, Z];
                    KaitenArrList[0][X, Y, Z] = SetVal;
                    KaitenArrList[1][X, Y, BaseUB_Z - Z] = SetVal;
                    KaitenArrList[2][X, BaseUB_Y - Y, Z] = SetVal;
                    KaitenArrList[3][X, BaseUB_Y - Y, BaseUB_Z - Z] = SetVal;
                    KaitenArrList[4][BaseUB_X - X, Y, Z] = SetVal;
                    KaitenArrList[5][BaseUB_X - X, Y, BaseUB_Z - Z] = SetVal;
                    KaitenArrList[6][BaseUB_X - X, BaseUB_Y - Y, Z] = SetVal;
                    KaitenArrList[7][BaseUB_X - X, BaseUB_Y - Y, BaseUB_Z - Z] = SetVal;

                    KaitenArrList[8][X, Z, Y] = SetVal;
                    KaitenArrList[9][X, Z, BaseUB_Y - Y] = SetVal;
                    KaitenArrList[10][X, BaseUB_Z - Z, Y] = SetVal;
                    KaitenArrList[11][X, BaseUB_Z - Z, BaseUB_Y - Y] = SetVal;
                    KaitenArrList[12][BaseUB_X - X, Z, Y] = SetVal;
                    KaitenArrList[13][BaseUB_X - X, Z, BaseUB_Y - Y] = SetVal;
                    KaitenArrList[14][BaseUB_X - X, BaseUB_Z - Z, Y] = SetVal;
                    KaitenArrList[15][BaseUB_X - X, BaseUB_Z - Z, BaseUB_Y - Y] = SetVal;

                    KaitenArrList[16][Y, X, Z] = SetVal;
                    KaitenArrList[17][Y, X, BaseUB_Z - Z] = SetVal;
                    KaitenArrList[18][Y, BaseUB_X - X, Z] = SetVal;
                    KaitenArrList[19][Y, BaseUB_X - X, BaseUB_Z - Z] = SetVal;
                    KaitenArrList[20][BaseUB_Y - Y, X, Z] = SetVal;
                    KaitenArrList[21][BaseUB_Y - Y, X, BaseUB_Z - Z] = SetVal;
                    KaitenArrList[22][BaseUB_Y - Y, BaseUB_X - X, Z] = SetVal;
                    KaitenArrList[23][BaseUB_Y - Y, BaseUB_X - X, BaseUB_Z - Z] = SetVal;

                    KaitenArrList[24][Y, Z, X] = SetVal;
                    KaitenArrList[25][Y, Z, BaseUB_X - X] = SetVal;
                    KaitenArrList[26][Y, BaseUB_Z - Z, X] = SetVal;
                    KaitenArrList[27][Y, BaseUB_Z - Z, BaseUB_X - X] = SetVal;
                    KaitenArrList[28][BaseUB_Y - Y, Z, X] = SetVal;
                    KaitenArrList[29][BaseUB_Y - Y, Z, BaseUB_X - X] = SetVal;
                    KaitenArrList[30][BaseUB_Y - Y, BaseUB_Z - Z, X] = SetVal;
                    KaitenArrList[31][BaseUB_Y - Y, BaseUB_Z - Z, BaseUB_X - X] = SetVal;

                    KaitenArrList[32][Z, X, Y] = SetVal;
                    KaitenArrList[33][Z, X, BaseUB_Y - Y] = SetVal;
                    KaitenArrList[34][Z, BaseUB_X - X, Y] = SetVal;
                    KaitenArrList[35][Z, BaseUB_X - X, BaseUB_Y - Y] = SetVal;
                    KaitenArrList[36][BaseUB_Z - Z, X, Y] = SetVal;
                    KaitenArrList[37][BaseUB_Z - Z, X, BaseUB_Y - Y] = SetVal;
                    KaitenArrList[38][BaseUB_Z - Z, BaseUB_X - X, Y] = SetVal;
                    KaitenArrList[39][BaseUB_Z - Z, BaseUB_X - X, BaseUB_Y - Y] = SetVal;

                    KaitenArrList[40][Z, Y, X] = SetVal;
                    KaitenArrList[41][Z, Y, BaseUB_X - X] = SetVal;
                    KaitenArrList[42][Z, BaseUB_Y - Y, X] = SetVal;
                    KaitenArrList[43][Z, BaseUB_Y - Y, BaseUB_X - X] = SetVal;
                    KaitenArrList[44][BaseUB_Z - Z, Y, X] = SetVal;
                    KaitenArrList[45][BaseUB_Z - Z, Y, BaseUB_X - X] = SetVal;
                    KaitenArrList[46][BaseUB_Z - Z, BaseUB_Y - Y, X] = SetVal;
                    KaitenArrList[47][BaseUB_Z - Z, BaseUB_Y - Y, BaseUB_X - X] = SetVal;
                }
            }
        }

        //Distinctする
        for (int I = KaitenArrList.Count - 1; 0 <= I; I--) {
            for (int J = 0; J <= I - 1; J++) {
                //UBが違う場合は、同一でない
                if (KaitenArrList[I].GetUpperBound(0) != KaitenArrList[J].GetUpperBound(0)) continue;
                if (KaitenArrList[I].GetUpperBound(1) != KaitenArrList[J].GetUpperBound(1)) continue;
                if (KaitenArrList[I].GetUpperBound(2) != KaitenArrList[J].GetUpperBound(2)) continue;

                IEnumerable<bool> wkEnum1 = KaitenArrList[I].Cast<bool>();
                IEnumerable<bool> wkEnum2 = KaitenArrList[J].Cast<bool>();
                if (wkEnum1.SequenceEqual(wkEnum2) == false) continue;

                KaitenArrList.RemoveAt(I);
                break;
            }
        }
        return KaitenArrList;
    }

    //マス目にピースを埋めれるか
    static bool CanFillPiece(bool[, ,] pPieceMap,
        int pTargetX, int pTargetY, int pTargetZ, char[, ,] pBanArr)
    {
        if (pTargetX + pPieceMap.GetUpperBound(0) > UB_X) return false;
        if (pTargetY + pPieceMap.GetUpperBound(1) > UB_Y) return false;
        if (pTargetZ + pPieceMap.GetUpperBound(2) > UB_Z) return false;

        for (int X = 0; X <= pPieceMap.GetUpperBound(0); X++) {
            for (int Y = 0; Y <= pPieceMap.GetUpperBound(1); Y++) {
                for (int Z = 0; Z <= pPieceMap.GetUpperBound(2); Z++) {
                    if (pPieceMap[X, Y, Z]
                     && pBanArr[pTargetX + X, pTargetY + Y, pTargetZ + Z] != ' ')
                        return false;
                }
            }
        }
        return true;
    }

    //解を出力
    static void PrintAnswer(char[, ,] pBanArr)
    {
        var sb = new System.Text.StringBuilder();

        for (int Z = 0; Z <= UB_Z; Z++) {
            sb.AppendFormat("Z={0}の平面", Z);
            sb.AppendLine();
            for (int Y = 0; Y <= UB_Y; Y++) {
                for (int X = 0; X <= UB_X; X++) {
                    sb.Append(pBanArr[X, Y, Z]);
                }
                sb.AppendLine();
            }
        }
        Console.WriteLine(sb.ToString());
    }
}

実行結果

解1を発見。経過時間=00:00:06.1798178
Z=0の平面
VY
VI
V*
Z=1の平面
YY
FI
V*
Z=2の平面
FY
FI
V*
Z=3の平面
NY
FI
F*
Z=4の平面
NZ
NI
N*
Z=5の平面
WZ
WZ
N*
Z=6の平面
PP
WZ
W*
Z=7の平面
PP
XZ
W*
Z=8の平面
XP
XL
X*
Z=9の平面
UU
XL
T*
Z=10の平面
TU
TL
T*
Z=11の平面
UU
LL
T*

解説

回転解の除外で、Iペンタキューブは、Yが5以下の座標から配置するようにして、
深さ優先探索で解を列挙してます。