using System;
using System.Collections.Generic;
using System.Linq;
class Program
{
static void Main()
{
var sw = System.Diagnostics.Stopwatch.StartNew();
int AnswerCnt = 0;
int AnswerX = 0;
int AnswerY = 0;
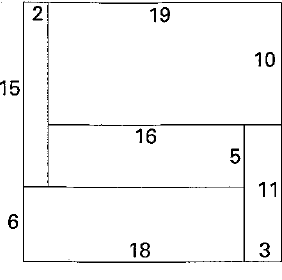
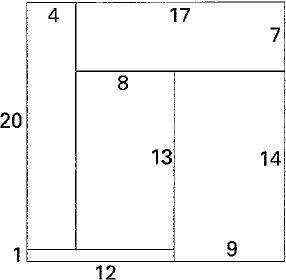
//家の横幅 <= 縦幅 としてループ
for (int X = 20 + 19; 1 + 2 <= X; X--) {
for (int Y = X; Y <= 20 + 19; Y++) {
Console.WriteLine("横{0},縦{1}の家の解を調査中。経過時間={2}", X, Y, sw.Elapsed);
if (X * Y < AnswerX * AnswerY) continue;
List<HeyaInfoDef[]> HeyaKouhoArrList =
DeriveHeyaKouhoArrList(X, Y);
int wkAnswerCnt = DeriveAnswer(HeyaKouhoArrList);
if (wkAnswerCnt > 0) {
Console.WriteLine("解は、{0}通り", wkAnswerCnt);
AnswerCnt = wkAnswerCnt;
AnswerX = X; AnswerY = Y;
}
}
}
Console.WriteLine("解は、横{0},縦{1}の場合で{2}通り", AnswerX, AnswerY, AnswerCnt);
}
//5つの部屋の候補から解を求めて、解の数を返す
static int DeriveAnswer(List<HeyaInfoDef[]> pHeyaKouhoArrList)
{
int AnswerCnt = 0;
for (int I = 0; I <= pHeyaKouhoArrList.Count - 1; I++) {
for (int J = I + 1; J <= pHeyaKouhoArrList.Count - 1; J++) {
var wkHashSet = new HashSet<int>();
wkHashSet.UnionWith(pHeyaKouhoArrList[I].Select(X => X.Yoko));
wkHashSet.UnionWith(pHeyaKouhoArrList[I].Select(X => X.Tate));
wkHashSet.UnionWith(pHeyaKouhoArrList[J].Select(X => X.Yoko));
wkHashSet.UnionWith(pHeyaKouhoArrList[J].Select(X => X.Tate));
//長さの個数が20でなかったらContinue
if (wkHashSet.Count < 20) continue;
AnswerCnt++;
//Console.WriteLine("解{0}を発見", ++AnswerCnt);
//DebugPrintHeya(pHeyaKouhoArrList[I]);
//DebugPrintHeya(pHeyaKouhoArrList[J]);
}
}
return AnswerCnt;
}
//部屋情報
struct HeyaInfoDef
{
internal int Yoko;
internal int Tate;
}
//家の横幅と縦幅を引数として、5つの部屋の候補を列挙
static List<HeyaInfoDef[]> DeriveHeyaKouhoArrList(int pIeYoko, int pIeTate)
{
var WillReturn = new List<HeyaInfoDef[]>();
//中央の部屋の横幅と縦幅でループ
for (int TyuuouYoko = 1; TyuuouYoko <= pIeYoko - 2; TyuuouYoko++) {
for (int TyuuouTate = 1; TyuuouTate <= pIeTate - 2; TyuuouTate++) {
//中央の部屋の配置(0ベース)でループ
for (int HaitiX = 1; ; HaitiX++) {
if (pIeYoko <= HaitiX + TyuuouYoko) break;
for (int HaitiY = 1; ; HaitiY++) {
if (pIeTate <= HaitiY + TyuuouTate) break;
WillReturn.Add(DeriveHeyaKouhoArr(
pIeYoko, pIeTate, TyuuouYoko, TyuuouTate, HaitiX, HaitiY));
}
}
}
}
//長さが21以上の部屋が存在したらRemove
WillReturn.RemoveAll(X => Array.Exists(X, A => A.Yoko >= 21 || A.Tate >= 21));
//同じ長さの部屋が存在したらNG
for (int I = WillReturn.Count - 1; 0 <= I; I--) {
var wkHashSet = new HashSet<int>();
wkHashSet.UnionWith(WillReturn[I].Select(X => X.Yoko));
wkHashSet.UnionWith(WillReturn[I].Select(X => X.Tate));
//長さの個数が10でなかったらRemove
if (wkHashSet.Count < 10)
WillReturn.RemoveAt(I);
}
//回転解の除外
for (int I = WillReturn.Count - 1; 0 <= I; I--) {
for (int J = 0; J <= I - 1; J++) {
//90度回転
bool WillRemove = true;
if (WillReturn[I][0].Yoko != WillReturn[J][0].Tate) WillRemove = false;
if (WillReturn[I][0].Tate != WillReturn[J][0].Yoko) WillRemove = false;
if (WillReturn[I][1].Yoko != WillReturn[J][2].Tate) WillRemove = false;
if (WillReturn[I][1].Tate != WillReturn[J][2].Yoko) WillRemove = false;
if (WillReturn[I][2].Yoko != WillReturn[J][3].Tate) WillRemove = false;
if (WillReturn[I][2].Tate != WillReturn[J][3].Yoko) WillRemove = false;
if (WillRemove) { WillReturn.RemoveAt(I); break; }
//180度回転
WillRemove = true;
if (WillReturn[I][0].Yoko != WillReturn[J][0].Yoko) WillRemove = false;
if (WillReturn[I][0].Tate != WillReturn[J][0].Tate) WillRemove = false;
if (WillReturn[I][1].Yoko != WillReturn[J][3].Yoko) WillRemove = false;
if (WillReturn[I][1].Tate != WillReturn[J][3].Tate) WillRemove = false;
if (WillReturn[I][2].Yoko != WillReturn[J][4].Yoko) WillRemove = false;
if (WillReturn[I][2].Tate != WillReturn[J][4].Tate) WillRemove = false;
if (WillRemove) { WillReturn.RemoveAt(I); break; }
//270度回転
WillRemove = true;
if (WillReturn[I][0].Yoko != WillReturn[J][0].Tate) WillRemove = false;
if (WillReturn[I][0].Tate != WillReturn[J][0].Yoko) WillRemove = false;
if (WillReturn[I][1].Yoko != WillReturn[J][4].Tate) WillRemove = false;
if (WillReturn[I][1].Tate != WillReturn[J][4].Yoko) WillRemove = false;
if (WillReturn[I][2].Yoko != WillReturn[J][1].Tate) WillRemove = false;
if (WillReturn[I][2].Tate != WillReturn[J][1].Yoko) WillRemove = false;
if (WillRemove) { WillReturn.RemoveAt(I); break; }
}
}
return WillReturn;
}
//家の横幅と縦幅、中央の部屋の横幅と縦幅、中央の部屋の配置を引数として、部屋情報の配列を作成
static HeyaInfoDef[] DeriveHeyaKouhoArr(int pIeYoko, int pIeTate,
int pTyuuouYoko, int pTyuuouTate, int pHaitiX, int pHaitiY)
{
var WillReturn = new List<HeyaInfoDef>();
Action<int, int> AddAct = (pYoko, pTate) =>
WillReturn.Add(new HeyaInfoDef() { Yoko = pYoko, Tate = pTate });
AddAct(pTyuuouYoko, pTyuuouTate); //中央の長方形
AddAct(pIeYoko - pHaitiX, pHaitiY); //右上の角の長方形
AddAct(pIeYoko - pHaitiX - pTyuuouYoko, pIeTate - pHaitiY); //右下の角の長方形
AddAct(pHaitiX + pTyuuouYoko, pIeTate - pHaitiY - pTyuuouTate); //左下の角の長方形
AddAct(pHaitiX, pHaitiY + pTyuuouTate); //左上の角の長方形
return WillReturn.ToArray();
}
//デバッグ用で家の部屋を出力
static void DebugPrintIe(List<HeyaInfoDef[]> pHeyaArrList)
{
for (int I = 0; I <= pHeyaArrList.Count - 1; I++) {
Console.Write("部屋{0}■", I + 1);
DebugPrintHeya(pHeyaArrList[I]);
}
}
//デバッグ用で部屋を出力
static void DebugPrintHeya(HeyaInfoDef[] pHeyaArr)
{
var sb = new System.Text.StringBuilder();
for (int I = 0; I <= pHeyaArr.GetUpperBound(0); I++) {
if (I == 0) sb.Append("中央");
if (I == 1) sb.Append("右上");
if (I == 2) sb.Append("右下");
if (I == 3) sb.Append("左下");
if (I == 4) sb.Append("左上");
sb.AppendFormat("横{0,2},縦{1,2},", pHeyaArr[I].Yoko, pHeyaArr[I].Tate);
}
Console.WriteLine(sb.ToString());
}
}