ABC-054-C One-stroke Path

■■■問題■■■

自己ループと二重辺を含まないN頂点M辺の重み無し無向グラフが与えられます。
i(1 <= i <= M) 番目の辺は頂点 ai と頂点 bi を結びます。
ここで、自己ループは ai=bi(1 <= i <= M) となる辺のことを表します。

また、二重辺は ai=aj かつ bi=bj(1 <= i<j <= M) となる辺のことを表します。
頂点1を始点として、全ての頂点を1度だけ訪れるパスは何通りありますか。
ただし、パスの始点と終点の頂点も訪れたものとみなします。

例として、図1のような無向グラフが与えられたとします。

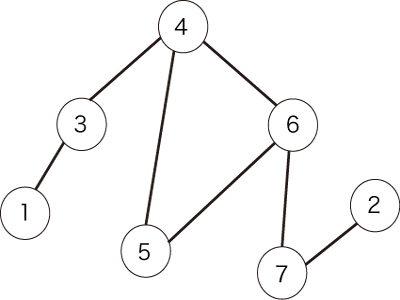図1：無向グラフの例

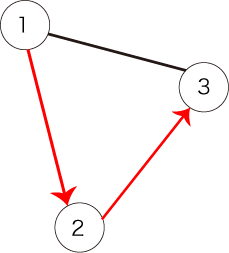
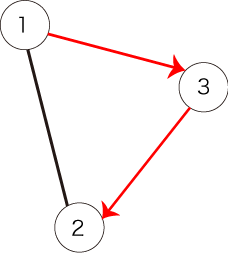
このとき、図2で表されるパスは条件を満たします。

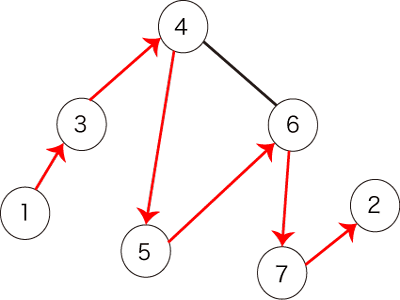図2：条件を満たすパスの例

しかし、図3で表されるパスは条件を満たしません。全ての頂点を訪れていないからです。

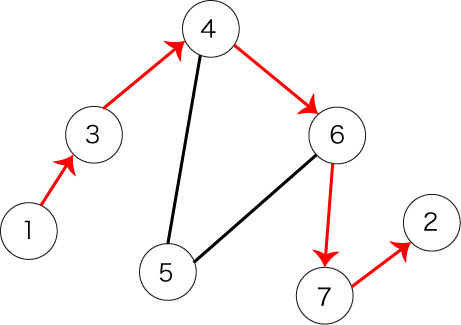図3：条件を満たさないパスの例1

また、図4で表されるパスも条件を満たしません。始点が頂点1ではないからです。

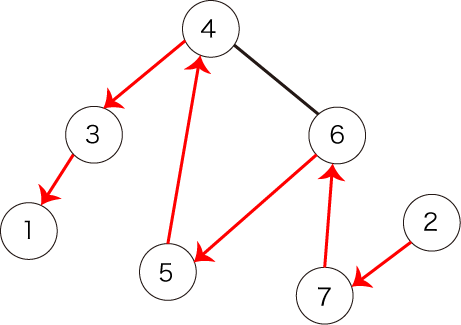図4：条件を満たさないパスの例2

■■■入力■■■

N M
a1 b1
a2 b2
・
・
・
aM bM

●2 <= N <= 8
●0 <= M <= N(N-1)/2
●1 <= ai<bi <= N
●与えられるグラフは自己ループと二重辺を含まない

■■■出力■■■

問題文の条件を満たすパスが何通りあるか出力せよ。

■■■サンプルケースのイメージ■■■

■入出力例1のイメージ■

与えられるグラフは以下の図で表されます。


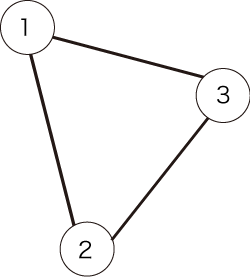条件を満たすパスは以下の2通りです。

C#のソース

using System;
using System.Collections.Generic;
using System.Linq;

class Program
{
    static string InputPattern = "InputX";

    static List<string> GetInputList()
    {
        var WillReturn = new List<string>();

        if (InputPattern == "Input1") {
            WillReturn.Add("3 3");
            WillReturn.Add("1 2");
            WillReturn.Add("1 3");
            WillReturn.Add("2 3");
            //2
        }
        else if (InputPattern == "Input2") {
            WillReturn.Add("7 7");
            WillReturn.Add("1 3");
            WillReturn.Add("2 7");
            WillReturn.Add("3 4");
            WillReturn.Add("4 5");
            WillReturn.Add("4 6");
            WillReturn.Add("5 6");
            WillReturn.Add("6 7");
            //1
            //このテストケースは問題文の例と同じです
        }
        else {
            string wkStr;
            while ((wkStr = Console.ReadLine()) != null) WillReturn.Add(wkStr);
        }
        return WillReturn;
    }

    struct JyoutaiDef
    {
        internal int CurrNode;
        internal HashSet<int> VisitedSet;
        //internal string Log;
    }

    static void Main()
    {
        List<string> InputList = GetInputList();

        int[] wkArr = { };
        Action<string> SplitAct = pStr =>
            wkArr = pStr.Split(' ').Select(X => int.Parse(X)).ToArray();

        SplitAct(InputList[0]);
        int N = wkArr[0];

        bool[,] EdgeArr = new bool[N + 1, N + 1];

        foreach (string EachStr in InputList.Skip(1)) {
            SplitAct(EachStr);
            EdgeArr[wkArr[0], wkArr[1]] = true;
        }

        var Stk = new Stack<JyoutaiDef>();
        JyoutaiDef WillPush;
        WillPush.CurrNode = 1;
        WillPush.VisitedSet = new HashSet<int>() { 1 };
        //WillPush.Log = "1";
        Stk.Push(WillPush);

        int AnswerCnt = 0;
        while (Stk.Count > 0) {
            JyoutaiDef Popped = Stk.Pop();

            //クリア判定
            if (Popped.VisitedSet.Count == N) {
                AnswerCnt++;
                //Console.WriteLine(Popped.Log);
                continue;
            }

            for (int I = 1; I <= N; I++) {
                //再訪不可
                if (Popped.VisitedSet.Contains(I)) continue;

                if (EdgeArr[Popped.CurrNode, I] || EdgeArr[I, Popped.CurrNode]) {
                    WillPush.CurrNode = I;
                    WillPush.VisitedSet = new HashSet<int>(Popped.VisitedSet);
                    WillPush.VisitedSet.Add(I);
                    //WillPush.Log = Popped.Log + "," + pNewNode.ToString();

                    Stk.Push(WillPush);
                }
            }
        }
        Console.WriteLine(AnswerCnt);
    }
}

解説

深さ優先探索で経路を全探索してます。