004 ダイクストラ法

下記の有向グラフでのノードAから各ノードまでの最短距離を
ダイクストラ法で求めます。

C#のソース

using System;
using System.Collections.Generic;
using System.Linq;

class Program
{
    struct GraphInfoDef
    {
        internal char FromPos;
        internal char ToPos;
        internal int Kyori;
    }

    static void Main()
    {
        var GraphInfoList = new List<GraphInfoDef>();
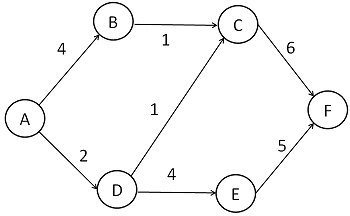
        GraphInfoList.Add(new GraphInfoDef() { FromPos = 'A', ToPos = 'B', Kyori = 4 });
        GraphInfoList.Add(new GraphInfoDef() { FromPos = 'A', ToPos = 'D', Kyori = 2 });
        GraphInfoList.Add(new GraphInfoDef() { FromPos = 'B', ToPos = 'C', Kyori = 1 });
        GraphInfoList.Add(new GraphInfoDef() { FromPos = 'C', ToPos = 'F', Kyori = 6 });
        GraphInfoList.Add(new GraphInfoDef() { FromPos = 'D', ToPos = 'C', Kyori = 1 });
        GraphInfoList.Add(new GraphInfoDef() { FromPos = 'D', ToPos = 'E', Kyori = 4 });
        GraphInfoList.Add(new GraphInfoDef() { FromPos = 'E', ToPos = 'F', Kyori = 5 });

        Dijkstra(GraphInfoList);
    }

    //ダイクストラ法で各ノードまでの最短距離を求める
    static void Dijkstra(List<GraphInfoDef> pGraphInfoList)
    {
        var PriorityQueue = new CppPriorityQueue();

        //確定ノードと距離合計のDict
        var KakuteiNodeDict = new Dictionary<char, int>();
        KakuteiNodeDict.Add('A', 0);

        //Enqueue処理
        Action<char> EnqueueAct = pFromPos =>
        {
            List<GraphInfoDef> wkGraphList =
                pGraphInfoList.FindAll(X => X.FromPos == pFromPos);
            foreach (GraphInfoDef EachGraphInfo in wkGraphList) {
                //確定ノードならContinue
                if (KakuteiNodeDict.ContainsKey(EachGraphInfo.ToPos)) continue;

                int wkSumKyori = KakuteiNodeDict[pFromPos] + EachGraphInfo.Kyori;
                PriorityQueue.Enqueue(wkSumKyori, EachGraphInfo.ToPos);
            }
        };
        EnqueueAct('A');

        while (PriorityQueue.Count > 0) {
            PriorityQueueItemDef Dequeued = PriorityQueue.Dequeue();
            //確定ノードならContinue
            if (KakuteiNodeDict.ContainsKey(Dequeued.Node)) continue;

            KakuteiNodeDict.Add(Dequeued.Node, Dequeued.SumKyori);
            EnqueueAct(Dequeued.Node);
        }

        foreach (var EachPair in KakuteiNodeDict.OrderBy(X => X.Value)) {
            Console.WriteLine("{0}までの最短距離は{1}", EachPair.Key, EachPair.Value);
        }
    }
}

//PriorityQueueもどき
struct PriorityQueueItemDef
{
    internal int SumKyori;
    internal char Node;
}
class CppPriorityQueue
{
    private List<PriorityQueueItemDef> mItemList = new List<PriorityQueueItemDef>();

    internal int Count { get { return mItemList.Count; } }

    internal void Enqueue(PriorityQueueItemDef pItem) { mItemList.Add(pItem); }

    internal void Enqueue(int pSumKyori, char pNode)
    {
        mItemList.Add(new PriorityQueueItemDef() { SumKyori = pSumKyori, Node = pNode });
    }

    internal PriorityQueueItemDef Dequeue()
    {
        int wkInd = 0;
        for (int I = 1; I <= mItemList.Count - 1; I++) {
            //距離合計が最小の要素を返す
            if (mItemList[I].SumKyori < mItemList[wkInd].SumKyori)
                wkInd = I;
        }
        PriorityQueueItemDef WillRetun = mItemList[wkInd];
        mItemList.RemoveAt(wkInd);
        return WillRetun;
    }
}

実行結果

Aまでの最短距離は0
Dまでの最短距離は2
Cまでの最短距離は3
Bまでの最短距離は4
Eまでの最短距離は6
Fまでの最短距離は9

解説

PriorityQueueのCountが0になるまでのループを
一番外側のループとしてます。