005 ワーシャルフロイド法

下記の有向グラフでのノードの組み合わせごとの最短距離を
ワーシャルフロイド法で求めます。

C#のソース

using System;
using System.Collections.Generic;

class Program
{
    struct GraphInfoDef
    {
        internal char FromPos;
        internal char ToPos;
        internal int Kyori;
    }

    static void Main()
    {
        var GraphInfoList = new List<GraphInfoDef>();
        GraphInfoList.Add(new GraphInfoDef() { FromPos = 'A', ToPos = 'B', Kyori = 4 });
        GraphInfoList.Add(new GraphInfoDef() { FromPos = 'A', ToPos = 'D', Kyori = 2 });
        GraphInfoList.Add(new GraphInfoDef() { FromPos = 'B', ToPos = 'C', Kyori = 1 });
        GraphInfoList.Add(new GraphInfoDef() { FromPos = 'C', ToPos = 'F', Kyori = 6 });
        GraphInfoList.Add(new GraphInfoDef() { FromPos = 'D', ToPos = 'C', Kyori = 1 });
        GraphInfoList.Add(new GraphInfoDef() { FromPos = 'D', ToPos = 'E', Kyori = 4 });
        GraphInfoList.Add(new GraphInfoDef() { FromPos = 'E', ToPos = 'F', Kyori = 5 });

        WarshallFloyd(GraphInfoList);
    }

    //ワーシャルフロイド法でノードの組み合わせごとの最短距離を求める
    static void WarshallFloyd(List<GraphInfoDef> pGraphInfoList)
    {
        var MinKyoriDict = new Dictionary<string, int>();

        //初期化処理
        for (char I = 'A'; I <= 'F'; I++) {
            for (char J = 'A'; J <= 'F'; J++) {
                string wkKey = string.Format("{0},{1}", I, J);

                if (I == J) {
                    MinKyoriDict[wkKey] = 0;
                }
                else {
                    int wkInd = pGraphInfoList.FindIndex(A => A.FromPos == I && A.ToPos == J);
                    if (wkInd >= 0)
                        MinKyoriDict[wkKey] = pGraphInfoList[wkInd].Kyori;
                    else MinKyoriDict[wkKey] = int.MaxValue / 2;
                }

            }
        }

        //ワーシャルフロイド法
        for (char K = 'A'; K <= 'F'; K++) {
            for (char I = 'A'; I <= 'F'; I++) {
                for (char J = 'A'; J <= 'F'; J++) {
                    string wkKey1 = string.Format("{0},{1}", I, J);
                    string wkKey2 = string.Format("{0},{1}", I, K);
                    string wkKey3 = string.Format("{0},{1}", K, J);

                    int CurrKyori1 = MinKyoriDict[wkKey1];
                    int CurrKyori2 = MinKyoriDict[wkKey2];
                    int CurrKyori3 = MinKyoriDict[wkKey3];

                    if (CurrKyori1 > CurrKyori2 + CurrKyori3)
                        MinKyoriDict[wkKey1] = CurrKyori2 + CurrKyori3;
                }
            }
        }

        foreach (var EachPair in MinKyoriDict) {
            if (EachPair.Value == 0) continue;
            if (EachPair.Value == int.MaxValue / 2) continue;

            Console.WriteLine("{0}={1}", EachPair.Key, EachPair.Value);
        }
    }
}

実行結果

A,B=4
A,C=3
A,D=2
A,E=6
A,F=9
B,C=1
B,F=7
C,F=6
D,C=1
D,E=4
D,F=7
E,F=5

解説

ワーシャルフロイド法は、全てのノードの組み合わせ
無向グラフなら nC2
有向グラフなら nP2
の中間ノードを含まない始点と終点だけのエッジを作ると考えて理解しました。

最短経路は、コスト合計が同じなら、経由ノードが少ない経路として
下記の無向グラフ考えてみます。



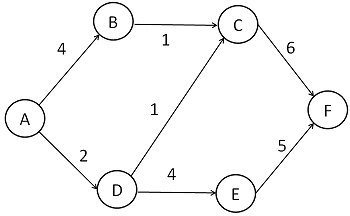
まず、Bを中間ノードに含む最短経路が存在しないようにするために
Bを経由した経路に着目して、エッジを追加します。
A-Cへのコストは、A-B-Cへのコストとします。



これによって、Bを中間ノードに含む最短経路が存在しないことになります。

次にCに着目します。
Cを中間ノードに含む最短経路が存在しないようにするために
Cを経由した経路に着目して、エッジを追加します。
B-Dへのコストは、B-C-Dへのコストとし、
A-Dへのコストは、A-C-Dへのコストとします。



これによって、Cを中間ノードに含む最短経路が存在しないことになります。

以上の処理を繰り返せば、
全てのノードの組み合わせで、
中間ノードを含まない最短距離であるエッジが作成されることになります。

なお、追加しようとしたエッジが既に存在する場合は、
コストの低いエッジを残すと考えます。(二重辺ができないイメージ)