CodeZineのMySQLの記事(シーズン2)の元原稿
第3回 SQLパズルの問題を解く
第1回 Window関数のサンプル集
第2回 MySQL8.0の再帰With句のサンプル集
今回のテーマ
MySQL8.0の新機能である再帰With句について解説します。
前半は、学習効率が良いと思われる順序で、再帰With句の各機能をイメージを交えて解説します。
後半は、バックトラック問題を解いたり、Oracleの再帰With句の機能をMySQL8.0で模倣する方法を解説します。
動作確認環境
MySQL 8.0.15
目次
01. With句とは
With句は、select文やupdate文やdelete文で、インラインビューを作成するという用途で使われます。
With句は、再帰のないWith句と、再帰のあるWith句(再帰With句)があります。
木構造や深さ優先探索や幅優先探索や有向グラフや無向グラフに関する知識があると、再帰With句を理解しやすいです。
02. 再帰のないWith句
再帰のないWith句の主な使い道は、3つあります。1つは、テスト用の仮想テーブルの作成です。
-- テスト用の仮想テーブルの作成
with work(Val1,Val2) as(
select 1,8 union all
select 2,9 union all
select 6,1)
select sum(Val1) as SumVal1,
sum(Val2) as SumVal2
from work;
出力結果
+---------+---------+
| SumVal1 | SumVal2 |
+---------+---------+
| 9 | 18 |
+---------+---------+
2つは、select文の結果を自己結合などで複数回使いたい時の2度書き防止です。
create table NonRecWithSample(ID char(3),Val int);
insert into NonRecWithSample values('AAA',100),
('AAA',300),
('BBB',500),
('CCC',100),
('DDD',200),
('DDD',700);
-- select文の2度書き防止
with tmp as(
select ID,sum(Val) as SumVal
from NonRecWithSample
group by ID)
select a.ID as a_ID,a.SumVal as a_SumVal,
b.ID as b_ID,b.SumVal as b_SumVal
from tmp a Join tmp b
on a.ID < b.ID
and a.SumVal < b.SumVal
order by a_ID,b_ID;
出力結果
+------+----------+------+----------+
| a_ID | a_SumVal | b_ID | b_SumVal |
+------+----------+------+----------+
| AAA | 400 | BBB | 500 |
| AAA | 400 | DDD | 900 |
| BBB | 500 | DDD | 900 |
| CCC | 100 | DDD | 900 |
+------+----------+------+----------+
3つは、インラインビューを含むSQLを、上から下に読めるようにすることによる、可読性の向上です。
-- インラインビューを含むSQL
select ID,Val
from (select ID,Val,
count(*) over(partition by ID) as cnt
from NonRecWithSample) a
where cnt = 1;
-- With句を使って、上から下に読めるようにしたSQL
with tmp as(
select ID,Val,
count(*) over(partition by ID) as cnt
from NonRecWithSample)
select ID,Val
from tmp
where cnt = 1;
03. 1から5までの整数を出力
1から5までの整数を出力してみます。なお、再帰のあるWith句では、recursiveキーワードが必須となります。
-- 1から5までの整数を出力
with recursive rec(Val) as(
select 1
union all
select Val+1
from rec
where Val+1 <= 5)
select Val from rec;
出力結果
+------+
| Val |
+------+
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
+------+
再帰With句では、union allの上を非再帰項と呼び、union allの下を再帰項と呼びます。
再帰With句は、
最初に非再帰項のselect文を実行して、
そのselect文の結果を使って再帰項のselect文を実行して、
そのselect文の結果を使って再帰項のselect文を実行して、
そのselect文の結果を使って再帰項のselect文を実行して、
(以下続く・・・)
といった処理を、再帰項のselect文の結果が0件になるまで行います。
上記のSQLでは、最初に非再帰項の select 1 で、1行作成してます。
次に再帰項において、select句のVal+1とwhere句のVal+1 <= 5で、
2から5までの整数を持つ行を作成してます。
非再帰項の段階での、SQLのイメージは下記となります。非再帰項による木の根の作成をイメージしてます。
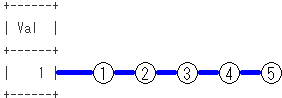
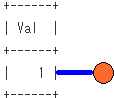再帰項の段階での、SQLのイメージは下記となります。再帰項による木のノードの作成をイメージしてます。
再帰With句の処理をイメージする際には、非再帰項と再帰項で2段階に分けてイメージすると分かりやすいです。
04. 再帰With句で行の分割
再帰With句で1行を複数行に分割してみます。
create table RowToRows(ID char(2),FromVal int,ToVal int);
insert into RowToRows values('AA',2,4),
('BB',8,9),
('CC',3,5);
IDごとに、FromValからToValまでの整数の行を作成します。
-- 1行を複数行に分割
with recursive rec(ID,FromVal,ToVal) as(
select ID,FromVal,ToVal
from RowToRows
union all
select ID,FromVal+1,ToVal
from rec
where FromVal+1 <= ToVal)
select ID,FromVal as Val from rec
order by ID,Val;
出力結果
+------+------+
| ID | Val |
+------+------+
| AA | 2 |
| AA | 3 |
| AA | 4 |
| BB | 8 |
| BB | 9 |
| CC | 3 |
| CC | 4 |
| CC | 5 |
+------+------+
再帰項でToValを上限として数値の加算を行って、行を再帰的に作成してます。
非再帰項の段階での、SQLのイメージは下記となります。非再帰項による木の根の作成をイメージしてます。
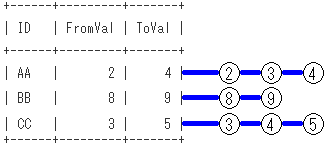
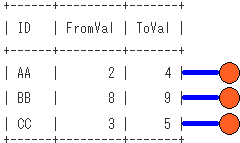再帰項の段階での、SQLのイメージは下記となります。再帰項による木のノードの作成をイメージしてます。
05. データ探索(木構造)
再帰With句で木構造なデータの探索を行うことができます。
create table TreeTable(ID int primary key,OyaID int);
insert into TreeTable values( 1,null),
( 2, 1),
( 3, 1),
( 4, 2),
( 5, 3),
(10,null),
(11, 10),
(12, 10);
木の根となる条件を、OyaID is null、親子条件を、親のID = 子のOyaID として木構造なデータを探索します。
根からの経路や、各ノードのレベルも求めます。
-- 木構造なデータの探索
with recursive rec(ID,OyaID,LV,Path) as(
select ID,OyaID,1,cast(ID as char(10))
from TreeTable
where OyaID is null
union all
select b.ID,b.OyaID,a.LV+1,
concat(a.Path , ',' , b.ID)
from rec a Join TreeTable b
on a.ID = b.OyaID)
select * from rec;
出力結果
+------+-------+------+-------+
| ID | OyaID | LV | Path |
+------+-------+------+-------+
| 1 | NULL | 1 | 1 |
| 10 | NULL | 1 | 10 |
| 2 | 1 | 2 | 1,2 |
| 3 | 1 | 2 | 1,3 |
| 11 | 10 | 2 | 10,11 |
| 12 | 10 | 2 | 10,12 |
| 4 | 2 | 3 | 1,2,4 |
| 5 | 3 | 3 | 1,3,5 |
+------+-------+------+-------+
非再帰項で、OyaIDがnullの行を木の根として出力して、
再帰項で、親子条件である、親のID = 子のOyaID を満たす行を再帰的に出力してます。
非再帰項の段階での、SQLのイメージは下記となります。非再帰項による木の根の作成をイメージしてます。
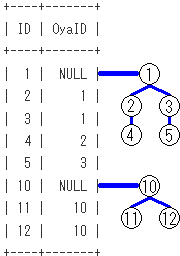
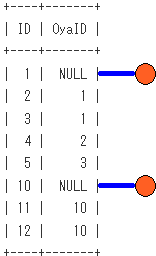再帰項の段階での、SQLのイメージは下記となります。再帰項による木のノードの作成をイメージしてます。
06. データ探索(有向グラフ)
再帰With句で有向グラフの探索を行うことができます。
create table GraphTable(ID int primary key,NextID int);
insert into GraphTable values(1,2),
(2,3),
(3,4),
(4,1),
(7,8),
(8,7);
ID = 1 のノードから到達可能なノードと、その経路を列挙してみます。
-- 閉路のある探索
with recursive rec(ID,NextID,Path) as(
select ID,NextID,cast(ID as char(10))
from GraphTable
where ID = 1
union all
select b.ID,b.NextID,concat(a.Path , ',' , b.ID)
from rec a Join GraphTable b
on a.NextID = b.ID
where Find_IN_Set(b.ID,a.Path) = false)
select * from rec;
出力結果
+------+--------+---------+
| ID | NextID | Path |
+------+--------+---------+
| 1 | 2 | 1 |
| 2 | 3 | 1,2 |
| 3 | 4 | 1,2,3 |
| 4 | 1 | 1,2,3,4 |
+------+--------+---------+
この有向グラフには、閉路(Cycle)が存在するので、
経路を記憶しつつ、Find_IN_Set関数で訪問済でないことをチェックしてます。
非再帰項の段階での、SQLのイメージは下記となります。
非再帰項による木の根の作成をイメージしてます。
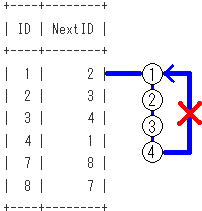
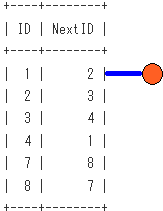再帰項の段階での、SQLのイメージは下記となります。
再帰項による木のノードの作成をイメージし、訪問済ノードへの再訪防止を赤バツでイメージしてます。
07. 枝切り(レベル制限)
再帰With句の探索の枝切りについて解説します。
create table LevelEdaKiri(ID int primary key,OyaID int);
insert into LevelEdaKiri values(10,null),
(11, 10),
(12, 11),
(13, 12),
(14, 13),
(31, 10),
(32, 31),
(33, 32);
ID = 10 の行から探索を始めて、到達可能なノードを表示します。ただし、ノードのレベルを3以下に制限します。
-- レベル制限で枝切り
with recursive rec(ID,OyaID,LV,Path) as(
select ID,OyaID,1,cast(ID as char(20))
from LevelEdaKiri
where ID = 10
union all
select b.ID,b.OyaID,a.LV+1,
concat(a.Path , ',' , b.ID)
from rec a Join LevelEdaKiri b
on a.ID = b.OyaID
where a.LV+1 <= 3)
select * from rec;
出力結果
+------+-------+------+----------+
| ID | OyaID | LV | Path |
+------+-------+------+----------+
| 10 | NULL | 1 | 10 |
| 11 | 10 | 2 | 10,11 |
| 31 | 10 | 2 | 10,31 |
| 12 | 11 | 3 | 10,11,12 |
| 32 | 31 | 3 | 10,31,32 |
+------+-------+------+----------+
上記のSQLのように、再帰項のwhere句で条件指定して枝切りを行うことができます。
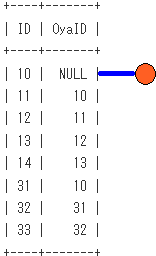
非再帰項の段階での、SQLのイメージは下記となります。非再帰項による木の根の作成をイメージしてます。
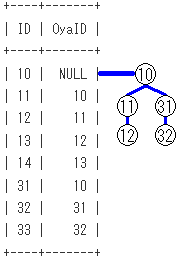
再帰項の段階での、SQLのイメージは下記となります。再帰項による木のノードの作成をイメージしてます。
08. 枝切り(外部結合後のwhere句)
再帰項での、外部結合後のwhere句で枝切りを行うこともできます。子ノードがなくても行を出力したい時に使います。
create table OuterJoinEdakiri(ID int primary key,OyaID int);
insert into OuterJoinEdakiri values( 1,null),
( 2, 1),
( 3, 2),
( 4, 3),
( 5, 3),
( 6, 2),
(30,null),
(31, 30),
(32, 30),
(33, 31),
(34, 33),
(60,null);
OyaID is null の行から探索を始めて、到達可能なノードを表示します。
ただし、ノードのレベルを3以下に制限し、
レベル1で到達可能なノード、
レベル2で到達可能なノード(なければnull)、
レベル3で到達可能なノード(なければnull)
をそれぞれ表示します。
-- 外部結合後のwhere句で枝切り
with recursive rec(TreeID,ID,OyaID,LV,Path) as(
select ID,ID,OyaID,1,cast(ID as char(20))
from OuterJoinEdakiri
where OyaID is null
union all
select a.TreeID,b.ID,b.OyaID,a.LV+1,
concat(a.Path , ',' , IfNull(b.ID,'null'))
from rec a Left Join OuterJoinEdakiri b
on a.ID = b.OyaID
where a.LV+1 <= 3)
select * from rec order by Path;
出力結果
+--------+------+-------+------+--------------+
| TreeID | ID | OyaID | LV | Path |
+--------+------+-------+------+--------------+
| 1 | 1 | NULL | 1 | 1 |
| 1 | 2 | 1 | 2 | 1,2 |
| 1 | 3 | 2 | 3 | 1,2,3 |
| 1 | 6 | 2 | 3 | 1,2,6 |
| 30 | 30 | NULL | 1 | 30 |
| 30 | 31 | 30 | 2 | 30,31 |
| 30 | 33 | 31 | 3 | 30,31,33 |
| 30 | 32 | 30 | 2 | 30,32 |
| 30 | NULL | NULL | 3 | 30,32,null |
| 60 | 60 | NULL | 1 | 60 |
| 60 | NULL | NULL | 2 | 60,null |
| 60 | NULL | NULL | 3 | 60,null,null |
+--------+------+-------+------+--------------+
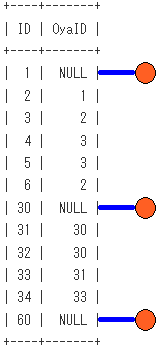
非再帰項の段階での、SQLのイメージは下記となります。非再帰項による木の根の作成をイメージしてます。
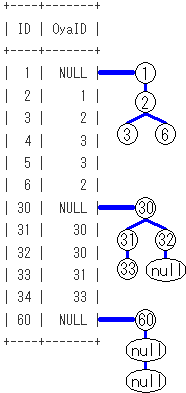
再帰項の段階での、SQLのイメージは下記となります。再帰項による木のノードの作成をイメージしてます。
09. 枝切り(union集合演算)
union集合演算の重複排除機能で枝切りを行うことができます。
create table UnionEdakiri(ID int primary key,Next1 int,Next2 int);
insert into UnionEdakiri values(10, 11, 13),
(11, 12, 14),
(12, 13,null),
(13, 11, 12),
(14, 10, 13),
(20, 21, 22);
ID = 10のノードから探索を開始して、訪問可能なノードを列挙してみます。レベルや経路などは表示しません。
-- union集合演算で枝切り
with recursive rec(ID,Next1,Next2) as(
select ID,Next1,Next2
from UnionEdakiri
where ID = 10
union
select b.ID,b.Next1,b.Next2
from rec a Join UnionEdakiri b
on b.ID in (a.Next1,a.Next2))
select * from rec;
出力結果
+------+-------+-------+
| ID | Next1 | Next2 |
+------+-------+-------+
| 10 | 11 | 13 |
| 11 | 12 | 14 |
| 13 | 11 | 12 |
| 12 | 13 | NULL |
| 14 | 10 | 13 |
+------+-------+-------+
再帰With句のselect句の列リストによっては、union集合演算で枝切りを行うと、
ループの検知などが不要になりシンプルなSQLとなります。
10. バックトラック問題(ナップサック問題)
再帰With句で、ナップサック問題を解いてみます。
最大で20kgまでの荷物を持てるとして、Valが最大になるIDの組み合わせを求めます。
create table nimotu(ID char(1) primary key,Val int,Kg int);
insert into nimotu values('A', 7,10),
('B', 2, 4),
('C', 9, 5),
('D', 4, 1),
('E', 9, 7),
('F', 7, 3),
('G', 4, 6),
('H', 5, 3);
-- ナップサック問題を解く
with recursive rec(ID,IDList,SumVal,SumKg) as(
select ID,cast(ID as char(20)),Val,Kg
from nimotu
union all
select b.ID,concat(a.IDList , ',' , b.ID),
a.SumVal+b.Val,a.SumKg+b.Kg
from rec a,nimotu b
where a.ID < b.ID
and a.SumKg + b.Kg <= 20)
select ID,IDList,SumVal,SumKg
from (select ID,IDList,SumVal,SumKg,
max(SumVal) over() as maxSumVal
from rec) a
where SumVal = maxSumVal;
出力結果
+------+-----------+--------+-------+
| ID | IDList | SumVal | SumKg |
+------+-----------+--------+-------+
| H | C,D,E,F,H | 34 | 19 |
+------+-----------+--------+-------+
再帰With句で20kg以下となる全ての組み合わせを求めてから、Window関数のmax関数でSumValの最大値を求めてます。
11. バックトラック問題(ナイト巡回問題)
再帰With句で、ナイト巡回問題を解いてみます。
create table Ban(X int,Y int);
insert into Ban
with tmp(Val) as(
select 1 union
select 2 union
select 3 union
select 4 union
select 5)
select a.Val,b.Val
from tmp a Cross Join tmp b;
-- ナイト巡回問題を解く
with recursive rec(X,Y,LV,Path) as(
select X,Y,1,cast(concat('(' , X , '-' , Y , ')') as char(200))
from Ban
where X = 1 and Y = 1
union all
select b.X,b.Y,a.LV+1,concat(a.Path , ',' , '(' , b.X , '-' , b.Y , ')')
from rec a,Ban b
where (b.X,b.Y) in ((a.X+2,a.Y+1),
(a.X+2,a.Y-1),
(a.X-2,a.Y+1),
(a.X-2,a.Y-1),
(a.X+1,a.Y+2),
(a.X+1,a.Y-2),
(a.X-1,a.Y+2),
(a.X-1,a.Y-2))
and Find_IN_Set(concat('(' , b.X , '-' , b.Y , ')') , a.Path) = false)
select Path
from rec
where LV = 5 * 5;
出力結果
+---------------------------------------------------------------+
| Path |
+---------------------------------------------------------------+
| (1-1),(2-3),(1-5),(3-4),(5-5),(4-3),(5-1),(3-2),(5-3),(4-1), |
| (2-2),(1-4),(3-5),(5-4),(4-2),(2-1),(1-3),(2-5),(4-4),(5-2), |
| (3-3),(4-5),(2-4),(1-2),(3-1) |
解は304通りあるので、1個目の解を、適宜改行して表示してます。
経路を記憶しつつ、Find_IN_Set関数で訪問済でないことをチェックしてます。
12. OracleのSearch句(深さ優先探索)を模倣
create table DepthFirstT(ID int primary key,OyaID int);
insert into DepthFirstT values( 1,null);
insert into DepthFirstT values( 2, 1);
insert into DepthFirstT values( 3, 1);
insert into DepthFirstT values( 4, 1);
insert into DepthFirstT values( 5, 3);
insert into DepthFirstT values( 6, 3);
insert into DepthFirstT values( 7, 4);
insert into DepthFirstT values( 8, 4);
insert into DepthFirstT values( 9, 6);
insert into DepthFirstT values(10, 7);
insert into DepthFirstT values(20,null);
insert into DepthFirstT values(21, 20);
insert into DepthFirstT values(22, 20);
insert into DepthFirstT values(23, 21);
insert into DepthFirstT values(24, 21);
Oracleの再帰With句では、Search句を使って、深さ優先探索順にソートできます。
MySQL 8.0で、下記のOracleのSQLと同じ結果を取得してみます。
-- 模倣対象のOracleのSQL
with rec(TreeID,ID,OyaID,LV,Path) as(
select ID,ID,OyaID,1,to_char(ID)
from DepthFirstT
where OyaID is null
union all
select a.TreeID,b.ID,b.OyaID,a.LV+1,a.Path || ',' || to_char(b.ID)
from rec a,DepthFirstT b
where a.ID = b.OyaID)
search depth first by ID desc set SortKey
select TreeID,ID,OyaID,LV,Path from rec
order by SortKey;
出力結果
TreeID ID OyaID LV Path
------ -- ----- -- --------
20 20 null 1 20
20 22 20 2 20,22
20 21 20 2 20,21
20 24 21 3 20,21,24
20 23 21 3 20,21,23
1 1 null 1 1
1 4 1 2 1,4
1 8 4 3 1,4,8
1 7 4 3 1,4,7
1 10 7 4 1,4,7,10
1 3 1 2 1,3
1 6 3 3 1,3,6
1 9 6 4 1,3,6,9
1 5 3 3 1,3,5
1 2 1 2 1,2
-- Search句(深さ優先探索)を模倣
with recursive tmp as(
select ID,OyaID,
LPad(Row_Number() over(order by ID desc),3,'0') as rn
from DepthFirstT),
rec(TreeID,ID,OyaID,LV,Path,SortStr) as(
select ID,ID,OyaID,1,
cast(ID as char(200)),
cast(rn as char(200))
from tmp
where OyaID is null
union all
select a.TreeID,b.ID,b.OyaID,a.LV+1,
concat(a.Path , ',' , b.ID),
concat(a.SortStr , ',' , b.rn)
from rec a Join tmp b
on a.ID = b.OyaID)
select * from rec order by SortStr;
出力結果
+--------+------+-------+------+----------+-----------------+
| TreeID | ID | OyaID | LV | Path | SortStr |
+--------+------+-------+------+----------+-----------------+
| 20 | 20 | NULL | 1 | 20 | 005 |
| 20 | 22 | 20 | 2 | 20,22 | 005,003 |
| 20 | 21 | 20 | 2 | 20,21 | 005,004 |
| 20 | 24 | 21 | 3 | 20,21,24 | 005,004,001 |
| 20 | 23 | 21 | 3 | 20,21,23 | 005,004,002 |
| 1 | 1 | NULL | 1 | 1 | 015 |
| 1 | 4 | 1 | 2 | 1,4 | 015,012 |
| 1 | 8 | 4 | 3 | 1,4,8 | 015,012,008 |
| 1 | 7 | 4 | 3 | 1,4,7 | 015,012,009 |
| 1 | 10 | 7 | 4 | 1,4,7,10 | 015,012,009,006 |
| 1 | 3 | 1 | 2 | 1,3 | 015,013 |
| 1 | 6 | 3 | 3 | 1,3,6 | 015,013,010 |
| 1 | 9 | 6 | 4 | 1,3,6,9 | 015,013,010,007 |
| 1 | 5 | 3 | 3 | 1,3,5 | 015,013,011 |
| 1 | 2 | 1 | 2 | 1,2 | 015,014 |
+--------+------+-------+------+----------+-----------------+
search depth first by ID desc set SortKeyを模倣するので、
最初に、Row_Number関数でIDの降順でのサロゲートキーに、LPad関数で前ゼロを付け、列別名rnとしてます。
次に、根からの経路上のrnをSortStrという列に追加していき、
最後に、order by SortStrとしてます。
13. OracleのSearch句(幅優先探索)を模倣
create table BreadthFirstT(ID int primary key,OyaID int);
insert into BreadthFirstT values( 1,null);
insert into BreadthFirstT values( 2, 1);
insert into BreadthFirstT values( 3, 1);
insert into BreadthFirstT values( 8, 2);
insert into BreadthFirstT values( 9, 2);
insert into BreadthFirstT values( 5, 3);
insert into BreadthFirstT values( 6, 3);
insert into BreadthFirstT values(30,null);
insert into BreadthFirstT values(31, 30);
Oracleの再帰With句では、Search句を使って、幅優先探索順にソートできます。
MySQL 8.0で、下記のOracleのSQLと同じ結果を取得してみます。
-- 模倣対象のOracleのSQL
with rec(ID,OyaID,LV,Path) as(
select ID,OyaID,1,to_char(ID)
from BreadthFirstT
where OyaID is null
union all
select b.ID,b.OyaID,a.LV+1,a.Path || ',' || to_char(b.ID)
from rec a,BreadthFirstT b
where a.ID = b.OyaID)
search breadth first by ID set SortKey
select ID,OyaID,LV,Path from rec
order by SortKey;
出力結果
ID OyaID LV Path
-- ----- -- -----
1 null 1 1
30 null 1 30
2 1 2 1,2
3 1 2 1,3
31 30 2 30,31
5 3 3 1,3,5
6 3 3 1,3,6
8 2 3 1,2,8
9 2 3 1,2,9
-- Search句(幅優先探索)を模倣
with recursive rec(ID,OyaID,LV,Path) as(
select ID,OyaID,1,cast(ID as char(200))
from BreadthFirstT
where OyaID is null
union all
select b.ID,b.OyaID,a.LV+1,concat(a.Path , ',' , b.ID)
from rec a Join BreadthFirstT b
on a.ID = b.OyaID)
select * from rec order by LV,ID;
search breadth first by ID set SortKeyでの幅優先探索を模倣するので、
ノードのレベルを第1ソートキーとし、IDの値を第2ソートキーにしてます。
14. OracleのCycle句を模倣
create table CycleT(ID int primary key,NextID int);
insert into CycleT values(1,2);
insert into CycleT values(2,3);
insert into CycleT values(3,4);
insert into CycleT values(4,1);
insert into CycleT values(5,5);
insert into CycleT values(7,8);
insert into CycleT values(8,7);
Oracleの再帰With句では、Cycle句を使って、閉路を検知することができます。
MySQL 8.0で、下記のOracleのSQLと同じ結果を取得してみます。
-- 模倣対象のOracleのSQL
with rec(ID,NextID,Path) as(
select ID,NextID,to_char(ID)
from CycleT
where ID in(1,5,7)
union all
select b.ID,b.NextID,a.Path || ',' || to_char(b.ID)
from rec a,CycleT b
where a.NextID = b.ID)
CYCLE ID SET IsLoop TO 'Y' DEFAULT 'N'
select ID,NextID,Path,IsLoop
from rec
order by Path;
出力結果
ID NextID Path IsLoop
-- ------ --------- ------
1 2 1 N
2 3 1,2 N
3 4 1,2,3 N
4 1 1,2,3,4 N
1 2 1,2,3,4,1 Y
5 5 5 N
5 5 5,5 Y
7 8 7 N
8 7 7,8 N
7 8 7,8,7 Y
-- Cycle句を模倣
with recursive rec(ID,NextID,Path,IsLoop) as(
select ID,NextID,cast(ID as char(20)),false
from CycleT
where ID in(1,5,7)
union all
select b.ID,b.NextID,concat(a.Path , ',' , b.ID),
Find_IN_Set(b.ID,a.Path)
from rec a Join CycleT b
on a.NextID = b.ID
where a.IsLoop = false)
select ID,NextID,Path,
If(IsLoop,'Y','N') as IsLoop
from rec order by Path;
ループの検知のために、経路を記憶しつつ、Find_IN_Set関数で、訪問済かをチェックしてます。
15. ズンドコキヨシ
with recursive rec(LV,ZunDokoStr) as(
select 0,Cast('' as Char(4000))
union all
select LV+1,concat(ZunDokoStr,if(Rand() > 0.5 ,'ズン！','ドコ！'))
from rec
where LV = 0 or ZunDokoStr Not Like '%ズン！ズン！ズン！ズン！ドコ！')
select concat(ZunDokoStr,'キ・ヨ・シ！') as "ズンドコキヨシ"
from rec order by LV desc Limit 1;
出力結果
ズンドコキヨシ
------------------------------------------------
ドコ！ズン！ズン！ズン！ズン！ドコ！キ・ヨ・シ！
参考資料