OracleSQLパズル
明智重蔵のブログ
明智重蔵のTwitter
記事(CodeZine)
PostgreSQL window関数
PostgreSQLパズル
PostgreSQLの再帰SQLの使用例
概要
PostgreSQLの再帰SQLの使用例について、まとめたページです。
PostgreSQL9.0を対象としてます。
目次
第1部 再帰SQLの使用例
1. 再帰のないwith句
再帰のないwith句の主な使い道は、3つあります。
1つは、テスト用の仮想テーブルの作成です。下記がサンプルです。
-- sample1
with work(Val1,Val2) as(
values(1,3),
(1,5),
(2,6),
(2,5))
select * from work;
Val1 | Val2
------+------
1 | 3
1 | 5
2 | 6
2 | 5
2つは、select文の結果を自己結合などで複数回使いたい時の2度書き防止です。
下記がサンプルです。
create table TestTable1(ID,Val) as
values('AAA',100),
('AAA',200),
('BBB',500),
('CCC',100),
('DDD',200),
('DDD',600);
-- sample2
with tmp as(
select ID,sum(Val) as sumVal
from TestTable1
group by ID)
select a.ID as a_ID,a.sumVal as a_sumVal,
b.ID as b_ID,b.sumVal as b_sumVal
from tmp a Join tmp b
on a.ID < b.ID
and a.sumVal < b.sumVal
order by a_ID,b_ID;
a_ID | a_sumVal | b_ID | b_sumVal
------+----------+------+----------
AAA | 300 | BBB | 500
AAA | 300 | DDD | 800
BBB | 500 | DDD | 800
CCC | 100 | DDD | 800
3つは、インランビューを含むSQLを、上から下に読めるようにすることによる、可読性の向上です。
ただし、行数が2行増えますね。(with tmpの行の分とfrom句の行の分)
インラインビューの行数が10行を越えたら、with句を検討する価値があると思います。下記がサンプルです。
-- インラインビューを含むSQL
select ID,Val
from (select ID,Val,
count(*) over(partition by ID) as cnt
from TestTable1) a
where cnt=1;
-- with句を使って、上から下に読めるようにしたSQL
with tmp as(
select ID,Val,
count(*) over(partition by ID) as cnt
from TestTable1)
select ID,Val
from tmp
where cnt=1;
2. 1から5までの整数を出力
1から5までの整数を出力してみます。
なお、再帰のあるwith句では、recursiveキーワードが必須となります。
-- sample3
with recursive rec(Val) as(
values(1)
union all
select Val+1
from rec
where Val+1 <= 5)
select Val from rec;
Val
-----
1
2
3
4
5
再帰SQLでは、union allの上を非再帰項と呼び、
union allの下を再帰項と呼びます。
再帰SQLは、最初に非再帰項のselect文を実行して、
そのselect文の結果を使って再帰項のselect文を実行して、
そのselect文の結果を使って再帰項のselect文を実行して、
そのselect文の結果を使って再帰項のselect文を実行して、(以下続く・・・)
といった処理を、再帰項のselect文の結果が0件になるまで行います。
最初に、非再帰項のvalues(1)で1行作成してます。
次に再帰項において、select句のVal+1とwhere句のVal+1 <= 5で
2から5までの整数を持つ行を作成してます。
脳内のイメージ(第1段階)は、下記となります。
非再帰項による木の根の作成をイメージしてます。
脳内のイメージ(第2段階)は、下記となります。
再帰項による木のノードの作成をイメージしてます。
再帰SQLの処理を脳内でイメージする際には
非再帰項と再帰項で2段階に分けてイメージすると分かりやすいです。
■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
ちなみに、1から5までの整数を出力するのであれば、
下記のように、generate_series関数を使うと簡単です。
マニュアル --- 9.22. 集合を返す関数
-- generate_series関数
select Val
from generate_series(1,5) as work(Val);
3. 1から5までの総積を求める
1から5までの総積を求めてみます。
-- sample4
with recursive rec(Val,souseki) as(
values(1,1)
union all
select Val+1,souseki*(Val+1)
from rec
where Val+1 <= 5)
select souseki
from rec
where Val = 5;
souseki
---------
120
再帰項のselect句で掛け算を繰り返してますね。
脳内のイメージ(第1段階)は、下記となります。
非再帰項による木の根の作成をイメージしてます。
脳内のイメージ(第2段階)は、下記となります。
再帰項による木のノードの作成をイメージしてます。
4. 再帰SQLで行の分割
create table FromToTable(ID,FromDay,ToDay) as
values('AA',date '2010-08-03',date '2010-08-06'),
('BB',date '2010-11-14',date '2010-11-16'),
('CC',date '2010-08-05',date '2010-08-06');
再帰SQLでIDごとに、FromDayからToDayまでの各日付の行を作成します。
-- sample5
with recursive rec(ID,FromDay,ToDay) as(
select ID,FromDay,ToDay
from FromToTable
union all
select ID,FromDay+1,ToDay
from rec
where FromDay+1 <= ToDay)
select ID,FromDay from rec
order by ID,FromDay;
ID | FromDay
----+------------
AA | 2010-08-03
AA | 2010-08-04
AA | 2010-08-05
AA | 2010-08-06
BB | 2010-11-14
BB | 2010-11-15
BB | 2010-11-16
CC | 2010-08-05
CC | 2010-08-06
再帰項でToDayを上限として日付の加算を行って、行を再帰的に作成してます。
脳内のイメージ(第1段階)は、下記となります。
非再帰項による木の根の作成をイメージしてます。
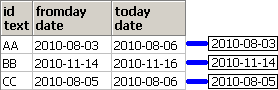脳内のイメージ(第2段階)は、下記となります。
再帰項による木のノードの作成をイメージしてます。
5. 木構造なデータの探索
create table IDTable(ID,OyaID) as
values( 1,null),
( 2, 1),
( 3, 1),
( 4, 2),
( 5, 2),
( 6, 3),
( 7, 6),
( 8, 6),
(50,null),
(55, 50),
(56, 50),
(58, 56);
OyaIDがnullの行を木の根として、
親子条件を (親の行の)ID = (子の行の)OyaID とし、木構造なデータを探索してみます。
根からの経路や、各ノードのレベルも求めます。
-- sample6
with recursive rec(ID,OyaID,path) as(
select ID,OyaID,array[ID]
from IDTable
where OyaID is null
union all
select b.ID,b.OyaID,path || b.ID
from rec a Join IDTable b
on a.ID = b.OyaID)
select ID,OyaID,path,array_upper(path,1) as LV
from rec order by path;
ID | OyaID | path | LV
----+-------+------------+----
1 | null | {1} | 1
2 | 1 | {1,2} | 2
4 | 2 | {1,2,4} | 3
5 | 2 | {1,2,5} | 3
3 | 1 | {1,3} | 2
6 | 3 | {1,3,6} | 3
7 | 6 | {1,3,6,7} | 4
8 | 6 | {1,3,6,8} | 4
50 | null | {50} | 1
55 | 50 | {50,55} | 2
56 | 50 | {50,56} | 2
58 | 56 | {50,56,58} | 3
非再帰項で、OyaIDがnullの行を木の根として出力して、
再帰項で、親子条件である、(親の行の)ID = (子の行の)OyaID を満たす行を再帰的に出力してます。
そして、根からの経路や、各ノードのレベルは、経路を記憶させた配列型を使って求めてます。
PostgreSQLの再帰SQLは、SQL99の配列型と組み合わせると非常に強力になります。
マニュアル --- 4.2.11. 配列コンストラクタ
マニュアル --- 8.14. 配列
マニュアル --- 9.17. 配列関数と演算子
脳内のイメージ(第1段階)は、下記となります。
非再帰項による木の根の作成をイメージしてます。
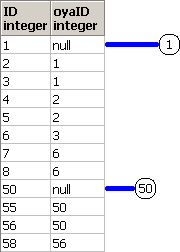脳内のイメージ(第2段階)は、下記となります。
再帰項による木のノードの作成をイメージしてます。
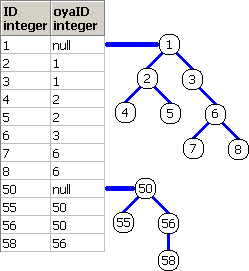
6. 有向グラフの探索
create table GraphTable(ID,NextID) as
values(1,2),
(2,3),
(3,4),
(4,1),
(7,8),
(8,7);
ID=1 のノードから到達可能なノードと、その経路を列挙してみます。
-- sample7
with recursive rec(ID,NextID,Path) as(
select ID,NextID,array[ID]
from GraphTable
where ID = 1
union all
select b.ID,b.NextID,a.Path || b.ID
from rec a,GraphTable b
where a.NextID = b.ID
and b.ID != all(a.Path))
select ID,NextID,Path from rec;
ID | NextID | Path
----+--------+-----------
1 | 2 | {1}
2 | 3 | {1,2}
3 | 4 | {1,2,3}
4 | 1 | {1,2,3,4}
この有向グラフには、閉路(Cycle)が存在するので、
経路を記憶させた配列型に対してall述語を使って、訪問済でないことを親子条件に追加してます。
脳内のイメージ(第1段階)は、下記となります。
非再帰項による木の根の作成をイメージしてます。
脳内のイメージ(第2段階)は、下記となります。
再帰項による木のノードの作成をイメージし、
訪問済ノードへの再訪防止を赤バツでイメージしてます。
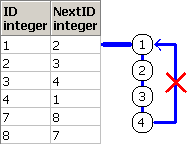
第2部 枝切り
7. 枝切り (レベル制限)
create table Edakiri1(ID,OyaID) as(
values(10,null),
(11, 10),
(12, 11),
(13, 12),
(14, 13),
(31, 10),
(32, 31),
(33, 32));
ID=10 の行から探索を始めて、到達可能なノードを表示します。
ただし、ノードのレベルを3以下に制限します。
-- sample8
with recursive rec(ID,OyaID,LV,Path) as(
select ID,OyaID,1,array[ID]
from Edakiri1
where ID=10
union all
select b.ID,b.OyaID,a.LV+1,a.Path || b.ID
from rec a,Edakiri1 b
where a.ID = b.OyaID
and a.LV+1 <= 3)
select * from rec;
ID | OyaID | LV | Path
----+-------+----+------------
10 | null | 1 | {10}
11 | 10 | 2 | {10,11}
31 | 10 | 2 | {10,31}
12 | 11 | 3 | {10,11,12}
32 | 31 | 3 | {10,31,32}
仮想表recにLVという列を追加して、1ずつ足し算を行ってます。
脳内のイメージ(第1段階)は、下記となります。
非再帰項による木の根の作成をイメージしてます。
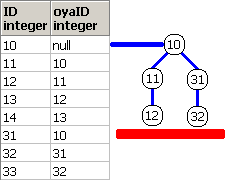
脳内のイメージ(第2段階)は、下記となります。
再帰項による木のノードの作成をイメージし、
ノードのレベル制限を超極太赤線でイメージしてます。
■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
経路を配列型で記憶させている場合は、
下記のSQLのように、array_length関数で各ノードのレベルを求めることもできます。
-- sample9
with recursive rec(ID,OyaID,Path) as(
select ID,OyaID,array[ID]
from Edakiri1
where ID=10
union all
select b.ID,b.OyaID,a.Path || b.ID
from rec a,Edakiri1 b
where a.ID = b.OyaID
and array_length(a.Path,1)+1 <= 3)
select * from rec;
ID | OyaID | Path
----+-------+------------
10 | null | {10}
11 | 10 | {10,11}
31 | 10 | {10,31}
12 | 11 | {10,11,12}
32 | 31 | {10,31,32}
8. 枝切り(外部結合後のwhere句)
create table Edakiri2(ID,OyaID) as
values( 1,null),
( 2, 1),
( 3, 2),
( 4, 3),
( 5, 3),
( 6, 2),
(80,null),
(81, 80),
(82, 80),
(83, 81),
(84, 83);
OyaID is null の行から探索を始めて、到達可能なノードを表示します。
ただし、ノードのレベルを3以下に制限し、
レベル1で到達可能なノード
レベル2で到達可能なノード(なければnull)
レベル3で到達可能なノード(なければnull)
をそれぞれ表示します。
-- sample10
with recursive rec(ID,OyaID,LV,Path) as(
select ID,OyaID,1,array[ID]
from Edakiri2
where OyaID is null
union all
select b.ID,b.OyaID,a.LV+1,a.Path || b.ID
from rec a Left Join Edakiri2 b
on a.ID = b.OyaID
where a.LV+1 <= 3)
select * from rec order by Path;
ID | OyaID | LV | Path
----+-------+----+--------------
1 | null | 1 | {1}
2 | 1 | 2 | {1,2}
3 | 2 | 3 | {1,2,3}
6 | 2 | 3 | {1,2,6}
80 | null | 1 | {80}
81 | 80 | 2 | {80,81}
83 | 81 | 3 | {80,81,83}
82 | 80 | 2 | {80,82}
null| null | 3 | {80,82,null}
あまり使い道はないと思いますが、
上記のように外部結合後のwhere句で枝切りを行うことも可能です。
脳内のイメージ(第1段階)は、下記となります。
非再帰項による木の根の作成をイメージしてます。
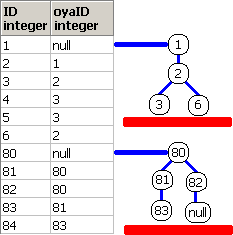
脳内のイメージ(第2段階)は、下記となります。
再帰項による木のノードの作成をイメージし、
ノードのレベル制限を超極太赤線でイメージしてます。
9. 枝切り(ノード数の総合計)
create table Edakiri3(Val) as(
select * from generate_series(1,10));
Valが3以下の行を木の根として、
親子条件を (親の行の)Val + 1 = (子の行の)Val とし、
幅優先探索でのノード数の総合計が10を超えたら、探索を打ち切ってみます。
-- sample11
with recursive rec(RootVal,Val,Path,nodeSum) as(
select Val,Val,array[Val],count(*) over()
from Edakiri3
where Val <= 3
union all
select a.RootVal,b.Val,a.Path || b.Val,
a.nodeSum+count(*) over()
from rec a,Edakiri3 b
where a.Val+1=b.Val
and a.nodeSum <= 10)
select * from rec;
RootVal | Val | Path | nodeSum
---------+-----+-----------+---------
1 | 1 | {1} | 3
2 | 2 | {2} | 3
3 | 3 | {3} | 3
1 | 2 | {1,2} | 6
2 | 3 | {2,3} | 6
3 | 4 | {3,4} | 6
1 | 3 | {1,2,3} | 9
2 | 4 | {2,3,4} | 9
3 | 5 | {3,4,5} | 9
1 | 4 | {1,2,3,4} | 12
2 | 5 | {2,3,4,5} | 12
3 | 6 | {3,4,5,6} | 12
PostgreSQLの再帰SQLでは、再帰項のselect句でwindow関数を使うことができますので、
window関数のcount関数を使用して、同一レベルでのノード数を求めてます。
10. 枝切り(他の木で訪問済なら訪問を回避)
create table Edakiri4(ID,Next1,Next2) as(
values(10, 11, 13),
(11, 12, 20),
(12, 13,null),
(13, 11, 12),
(14,null,null),
(20, 21, 22),
(22, 25, 26),
(25,null,null),
(26,null,null));
ID = 10のノードから探索を開始して、
訪問可能なノードと、最も短いレベルでの到達経路を表示します。
-- sample12
with recursive rec(ID,Next1,Next2,LV,Path,VisitedList) as(
select ID,Next1,Next2,1,array[ID],array[ID]
from Edakiri4
where ID = 10
union all
select b.ID,b.Next1,b.Next2,a.LV+1,a.Path || b.ID,
a.VisitedList || array_agg(b.ID) over()
from rec a,Edakiri4 b
where b.ID in (a.Next1,a.Next2)
and b.ID != all(a.VisitedList))
select * from rec;
ID | Next1 | Next2 | LV | Path | VisitedList
----+-------+-------+----+------------------+------------------------------
10 | 11 | 13 | 1 | {10} | {10}
11 | 12 | 20 | 2 | {10,11} | {10,11,13}
13 | 14 | null | 2 | {10,13} | {10,11,13}
12 | 13 | null | 3 | {10,11,12} | {10,11,13,12,20,14}
20 | 21 | 22 | 3 | {10,11,20} | {10,11,13,12,20,14}
14 | null | null | 3 | {10,13,14} | {10,11,13,12,20,14}
22 | 25 | 26 | 4 | {10,11,20,22} | {10,11,13,12,20,14,22}
25 | null | null | 5 | {10,11,20,22,25} | {10,11,13,12,20,14,22,25,26}
26 | null | null | 5 | {10,11,20,22,26} | {10,11,13,12,20,14,22,25,26}
再帰項でwindow関数のarray_agg関数を使って、別の木のノード一覧を取得し、
他の木で訪問済なら訪問を回避するのは、
エッジの重みが全て1な最短距離問題で使い道があるかもしれませんね。
11. 枝切り(union集合演算)
create table Edakiri5(ID,Next1,Next2) as(
values(10, 11, 13),
(11, 12, 14),
(12, 13,null),
(13, 11, 12),
(14, 10, 13),
(20, 21, 22));
ID = 10のノードから探索を開始して、訪問可能なノードを列挙してみます。
レベルや経路などは表示しません。
-- sample13
with recursive rec(ID,Next1,Next2) as(
select ID,Next1,Next2
from Edakiri5
where ID=10
union
select b.ID,b.Next1,b.Next2
from rec a,Edakiri5 b
where b.ID in (a.Next1,a.Next2))
select * from rec;
ID | Next1 | Next2
----+-------+-------
10 | 11 | 13
11 | 12 | 14
13 | 11 | 12
12 | 13 | null
14 | 10 | 13
マニュアルの7.8. WITH問い合わせに
再帰自己参照に対する作業テーブルの実行中の内容を置換し、再帰的表現を評価します。
UNION（しかしUNION ALLではない）に対し、重複行と前の結果行と重複する行を破棄します。
その再帰的問い合わせの結果の残っている全ての行を盛り込み、同時にそれらを暫定的中間テーブルに置きます。
と記述されているように、再帰SQLのselect句の列リストによっては、
union集合演算の重複排除機能で枝切りを行うと、ループの検知などが不要になりシンプルなSQLとなります。
12. 枝切り(Limit句)
-- sample14
with recursive rec(Val) as(
values(1)
union all
select Val+1
from rec)
select * from rec Limit 5;
Val
-----
1
2
3
4
5
マニュアルの7.8. WITH問い合わせに
ループするかどうか確信が持てない問い合わせをテストする有益な秘訣として、親問い合わせにLIMITを配置します。
これが動作するのは、PostgreSQLの実装が、
実際に親問い合わせで取り出されるのと同じ数のWITH問い合わせの行のみを評価するからです。
この秘訣を実稼動環境で使用することは勧められません。
と記述されているように、Limit句を使って枝切りをすることもできます。
実稼動環境で使用するのは避けたほうがいいと思いますが、
開発時に、再帰SQLの試行錯誤をする際に、Limit句を付けておくと便利です。
第3部 バックトラック問題
13. ナップサック問題
ナップサック問題を解いてみます。
最大で20kgまでの荷物を持てるとして、Valが最大になるIDの組み合わせを求めます。
create table nimotu(ID,Val,Kg) as
values(1, 7,10),
(2, 2, 4),
(3, 9, 5),
(4, 4, 1),
(5, 9, 7),
(6, 7, 3),
(7, 4, 6),
(8, 5, 3);
-- sample15
with recursive rec(ID,IDList,sumVal,SumKg) as(
select ID,array[ID],Val,Kg
from nimotu
union all
select b.ID,a.IDList || b.ID,
a.sumVal+b.Val,a.SumKg+b.Kg
from rec a,nimotu b
where a.ID < b.ID
and a.SumKg+b.Kg <= 20)
select ID,IDList,sumVal,sumKg
from (select ID,IDList,sumVal,sumKg,
max(sumVal) over() as maxSumVal
from rec) a
where sumVal = maxSumVal;
ID | IDList | sumVal | SumKg
----+-------------+--------+-------
8 | {3,4,5,6,8} | 34 | 19
再帰SQLで20kg以下となる全ての組み合わせを求めてから、
window関数のmax関数でsumValの最大値を求めてます。
もし、最大値を持つ行が1行だけであるならば、distinct onが使えます。
14. ナイト巡回問題
ナイト巡回問題を解いてみます。
create table ban(X,Y) as
select * from
generate_series(1,5) a,
generate_series(1,5) b;
-- sample16
with recursive rec(X,Y,LV,Path) as(
select X,Y,1,array[row(X,Y)]
from ban
where X=1 and Y=1
union all
select b.X,b.Y,a.LV+1,a.Path || row(b.X,b.y)
from rec a,ban b
where (b.X,b.Y) in ((a.X+2,a.Y+1),
(a.X+2,a.Y-1),
(a.X-2,a.Y+1),
(a.X-2,a.Y-1),
(a.X+1,a.Y+2),
(a.X+1,a.Y-2),
(a.X-1,a.Y+2),
(a.X-1,a.Y-2))
and row(b.X,b.y) != all(a.Path))
select Path
from rec
where LV = 5*5;
{(1,1),(2,3),(1,5),(3,4),(1,3),(2,1),(4,2),(5,4),(3,5),(1,4),(2,2),(4,1),(3,3),(2,5),(4,4),(5,2),(3,1),(1,2),(2,4),(4,5),(5,3),(3,2),(5,1),(4,3),(5,5)}
{(1,1),(2,3),(1,5),(3,4),(1,3),(2,1),(4,2),(5,4),(3,5),(1,4),(2,2),(4,1),(5,3),(4,5),(2,4),(1,2),(3,1),(5,2),(3,3),(2,5),(4,4),(3,2),(5,1),(4,3),(5,5)}
{(1,1),(2,3),(1,5),(3,4),(1,3),(2,1),(4,2),(5,4),(3,5),(1,4),(2,2),(4,1),(5,3),(4,5),(3,3),(2,5),(4,4),(5,2),(3,1),(1,2),(2,4),(3,2),(5,1),(4,3),(5,5)}
以下略
上記のSQLは、実行に5分かかりました。
木のノードを識別するキーが複数ある場合は、行コンストラクタを使うと効果的です。
15. strPos関数,subStr関数,OverLay関数
数独を解くのに使う文字列関数の紹介です。
-- sample17
select
strPos(Val,'a') as tes1,
strPos(Val,'X') as tes2,
subStr(Val,1,2) as tes3,
subStr(Val,3,2) as tes4,
OverLay(Val placing '000' from 2) as tes5,
OverLay(Val placing '000' from 2 for 0) as tes6
from (values('abcdef')) as work(Val);
tes1 | tes2 | tes3 | tes4 | tes5 | tes6
------+------+------+------+--------+-----------
1 | 0 | ab | cd | a000ef | a000bcdef
16. 数独
再帰SQLで、数独を解いてみます。
-- sample18
with recursive work(Val) as(
values('530070000'
|| '600195000'
|| '098000060'
|| '800060003'
|| '400803001'
|| '700020006'
|| '060000280'
|| '000419005'
|| '000080079')),
rec(LV,Val) as(
select 1,Val from work
union all
select LV+1,
case when subStr(Val,LV,1) = '0'
then overLay(Val placing cnt::text from LV)
else Val end
from rec a,generate_series(1,9) as b(cnt)
where LV <= 81
and (subStr(Val,LV,1) = '0' or b.cnt=1)
and (subStr(Val,LV,1) !='0'
or (strPos(subStr(Val,(LV-1)/9*9+1 ,9),cnt::text) = 0 /*横チェック*/
and strPos(subStr(Val,(LV-1)%9+1 ,1),cnt::text) = 0 /*縦チェック*/
and strPos(subStr(Val,(LV-1)%9+1+ 9,1),cnt::text) = 0
and strPos(subStr(Val,(LV-1)%9+1+18,1),cnt::text) = 0
and strPos(subStr(Val,(LV-1)%9+1+27,1),cnt::text) = 0
and strPos(subStr(Val,(LV-1)%9+1+36,1),cnt::text) = 0
and strPos(subStr(Val,(LV-1)%9+1+45,1),cnt::text) = 0
and strPos(subStr(Val,(LV-1)%9+1+54,1),cnt::text) = 0
and strPos(subStr(Val,(LV-1)%9+1+63,1),cnt::text) = 0
and strPos(subStr(Val,(LV-1)%9+1+72,1),cnt::text) = 0
and strPos(subStr(Val,((LV-1)%9)/3*3+1+9*(((LV-1)/9)/3*3) ,3),cnt::text) = 0 /*正方形チェック*/
and strPos(subStr(Val,((LV-1)%9)/3*3+1+9*(((LV-1)/9)/3*3)+ 9,3),cnt::text) = 0
and strPos(subStr(Val,((LV-1)%9)/3*3+1+9*(((LV-1)/9)/3*3)+18,3),cnt::text) = 0)))
select Val
from rec
where LV=82;
Val
---------------------------------------------------------------------------------
534678912672195348198342567859761423426853791713924856961537284287419635345286179
第4部 Oracleの再帰SQLの機能を模倣
17. Oracleのsearch句 (深さ優先探索)
create table siblingsT(
ID integer primary key,
OyaID integer);
insert into siblingsT values( 1,null);
insert into siblingsT values( 2, 1);
insert into siblingsT values( 3, 1);
insert into siblingsT values( 4, 1);
insert into siblingsT values( 5, 3);
insert into siblingsT values( 6, 3);
insert into siblingsT values( 7, 4);
insert into siblingsT values( 8, 4);
insert into siblingsT values( 9, 6);
insert into siblingsT values(10, 7);
insert into siblingsT values(20,null);
insert into siblingsT values(21, 20);
insert into siblingsT values(22, 20);
insert into siblingsT values(23, 21);
insert into siblingsT values(24, 21);
commit;
下記のsearch句(深さ優先探索)を使った、Oracle11gR2のSQLと同じ結果を取得する。
-- 模倣対象のOracle11gR2のSQL
col path for a10
with rec(treeID,ID,OyaID,LV,path) as(
select ID,ID,OyaID,1,to_char(ID)
from siblingsT
where OyaID is null
union all
select a.treeID,b.ID,b.OyaID,a.LV+1,a.path || ',' || to_char(b.ID)
from rec a,siblingsT b
where a.ID = b.OyaID)
search depth first by ID desc set SortKey
select treeID,ID,OyaID,LV,path from rec
order by SortKey;
treeID ID OyaID LV path
------ -- ----- -- --------
20 20 null 1 20
20 22 20 2 20,22
20 21 20 2 20,21
20 24 21 3 20,21,24
20 23 21 3 20,21,23
1 1 null 1 1
1 4 1 2 1,4
1 8 4 3 1,4,8
1 7 4 3 1,4,7
1 10 7 4 1,4,7,10
1 3 1 2 1,3
1 6 3 3 1,3,6
1 9 6 4 1,3,6,9
1 5 3 3 1,3,5
1 2 1 2 1,2
-- sample19
with recursive tmp as(
select ID,OyaID,
Row_Number() over(order by ID desc) as rn
from siblingsT),
rec(treeID,ID,OyaID,path,sortArray) as(
select ID,ID,OyaID,array[ID],array[rn]
from tmp
where OyaID is null
union all
select a.treeID,b.ID,b.OyaID,a.path || b.ID,
a.sortArray || b.rn
from rec a,tmp b
where a.ID = b.OyaID)
select treeID,ID,OyaID,
array_length(path,1) as LV,
array_to_string(path, ',') as path
from rec
order by sortArray;
search depth first by ID desc set SortKey
を模倣するので、まず、Row_Number関数でIDの降順の連番を列別名rnとして求めてます。
そして、根からの経路上のrnを配列型で保存していって、最後にorder byでソートキーとして使ってます。
配列型のソートの仕組み 9.17. 配列関数と演算子
■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
search depth firstの模倣ケースごとにまとめると下記となります。
search depth first byのソートキーに重複値がある場合、または、ソートキーがdesc指定を含む場合、
最初にRow_Number関数を使わなければいけません。
******************************************************************************
search depth first byのソートキーに重複値がある場合
最初にRow_Number関数を使って一意なソートキーを作成して列別名rnとし、
根からの経路上のrnを保存した配列を最後にorder byでソートキーとして使う。
******************************************************************************
search depth first byのソートキーが複数の場合
複数ソートキーを持つ行コンストラクタの配列に根からの経路を保存させて、
最後にorder byでソートキーとして使う。
******************************************************************************
search depth first byのソートキーがdesc指定を含む場合
最初にRow_Number関数でdesc指定を含むソートを使って、列別名rnとし、
根からの経路上のrnを保存した配列を最後にorder byでソートキーとして使う。
18. Oracleのsearch句 (幅優先探索)
create table BreadthFirstT(
ID integer primary key,
OyaID integer);
insert into BreadthFirstT values( 1,null);
insert into BreadthFirstT values( 2, 1);
insert into BreadthFirstT values( 3, 1);
insert into BreadthFirstT values( 8, 2);
insert into BreadthFirstT values( 9, 2);
insert into BreadthFirstT values( 5, 3);
insert into BreadthFirstT values( 6, 3);
insert into BreadthFirstT values(30,null);
insert into BreadthFirstT values(31, 30);
commit;
下記のsearch句(幅優先探索)を使った、Oracle11gR2のSQLと同じ結果を取得する。
-- 模倣対象のOracle11gR2のSQL
col path for a10
with rec(ID,OyaID,LV,path) as(
select ID,OyaID,1,to_char(ID)
from BreadthFirstT
where OyaID is null
union all
select b.ID,b.OyaID,a.LV+1,a.path || ',' || to_char(b.ID)
from rec a,BreadthFirstT b
where a.ID = b.OyaID)
search breadth first by ID set SortKey
select ID,OyaID,LV,path from rec
order by SortKey;
ID OyaID LV path
-- ----- -- -----
1 null 1 1
30 null 1 30
2 1 2 1,2
3 1 2 1,3
31 30 2 30,31
5 3 3 1,3,5
6 3 3 1,3,6
8 2 3 1,2,8
9 2 3 1,2,9
-- sample20
with recursive rec(ID,OyaID,path) as(
select ID,OyaID,array[ID]
from BreadthFirstT
where OyaID is null
union all
select b.ID,b.OyaID,a.path || b.ID
from rec a,BreadthFirstT b
where a.ID = b.OyaID)
select ID,OyaID,
array_length(path,1) as LV,
array_to_string(path, ',') as path
from rec
order by LV,ID;
幅優先探索なので、
ノードのレベルを第1ソートキーとし、
ノードの値を第2ソートキーにしてます。
19. Oracleのcycle句
create table CycleT(
ID integer primary key,
nextID integer);
insert into CycleT values(1,2);
insert into CycleT values(2,3);
insert into CycleT values(3,4);
insert into CycleT values(4,1);
insert into CycleT values(5,5);
insert into CycleT values(7,8);
insert into CycleT values(8,7);
commit;
下記のcycle句を使った、Oracle11gR2のSQLと同じ結果を取得する。
-- 模倣対象のOracle11gR2のSQL
col path for a10
col IsLoop for a10
with rec(ID,nextID,path) as(
select ID,nextID,to_char(ID)
from CycleT
where ID in(1,5,7)
union all
select b.ID,b.nextID,a.path || ',' || to_char(b.ID)
from rec a,CycleT b
where a.nextID = b.ID)
CYCLE ID SET IsLoop TO 'Y' DEFAULT 'N'
select ID,nextID,path,IsLoop
from rec
order by path;
ID nextID path IsLoop
-- ------ --------- ------
1 2 1 N
2 3 1,2 N
3 4 1,2,3 N
4 1 1,2,3,4 N
1 2 1,2,3,4,1 Y
5 5 5 N
5 5 5,5 Y
7 8 7 N
8 7 7,8 N
7 8 7,8,7 Y
-- sample21
with recursive rec(ID,nextID,path,IsLoop) as(
select ID,nextID,array[ID],false
from CycleT
where ID in(1,5,7)
union all
select b.ID,b.nextID,a.path || b.ID,
b.ID = any(a.path)
from rec a,CycleT b
where a.nextID = b.ID
and a.IsLoop = false)
select ID,NextID,
array_to_string(path, ',') as path,
case when IsLoop then 'Y' else 'N' end as IsLoop
from rec order by path;
ループの検知のために、訪問済のノードのIDを配列型に記憶させてます。
第5部 Oracleの階層問い合わせの機能を模倣
20. Level擬似列,prior演算子,connect_by_root演算子,sys_connect_by_path関数
create table HierarchicalT(
ID integer primary key,
OyaID integer);
insert into HierarchicalT values( 1,null);
insert into HierarchicalT values( 2, 1);
insert into HierarchicalT values( 3, 2);
insert into HierarchicalT values( 4, 3);
insert into HierarchicalT values( 5, 1);
insert into HierarchicalT values( 6, 5);
insert into HierarchicalT values( 7, 2);
insert into HierarchicalT values(20,null);
insert into HierarchicalT values(21, 20);
insert into HierarchicalT values(22, 21);
commit;
下記のLevel擬似列,prior演算子,connect_by_root演算子,sys_connect_by_path関数を使った、
Oracle11gR2のSQLと同じ結果を取得する。
-- 模倣対象のOracle11gR2のSQL
col path for a20
select ID,OyaID,
Level,prior ID as preID,
connect_by_root ID as rootID,
sys_connect_by_path(to_char(ID),',') as path
from HierarchicalT
start with OyaID is null
connect by prior ID = OyaID;
ID OyaID Level preID rootID path
-- ----- ----- ----- ------ ---------
1 null 1 null 1 ,1
2 1 2 1 1 ,1,2
3 2 3 2 1 ,1,2,3
4 3 4 3 1 ,1,2,3,4
7 2 3 2 1 ,1,2,7
5 1 2 1 1 ,1,5
6 5 3 5 1 ,1,5,6
20 null 1 null 20 ,20
21 20 2 20 20 ,20,21
22 21 3 21 20 ,20,21,22
-- sample22
with recursive rec(ID,OyaID,path) as(
select ID,OyaID,array[ID]
from HierarchicalT
where OyaID is null
union all
select b.ID,b.OyaID,a.path || b.ID
from rec a,HierarchicalT b
where a.ID = b.OyaID)
select ID,OyaID,
array_length(path,1) as LV,
path[array_length(path,1)-1] as preID,
path[1] as rootID,
',' || array_to_string(path, ',') as path
from rec
order by path;
マニュアル --- 9.17. 配列関数と演算子を駆使して、
Oracleの階層問い合わせの、
Level擬似列,prior演算子,connect_by_root演算子,sys_connect_by_path関数を模倣してます。
21. order siblings by
create table siblingsT2(
ID integer primary key,
OyaID integer);
insert into siblingsT2 values( 1,null);
insert into siblingsT2 values( 2, 1);
insert into siblingsT2 values( 3, 1);
insert into siblingsT2 values( 4, 1);
insert into siblingsT2 values( 5, 3);
insert into siblingsT2 values( 6, 3);
insert into siblingsT2 values( 7, 4);
insert into siblingsT2 values( 8, 4);
insert into siblingsT2 values( 9, 6);
insert into siblingsT2 values(10, 7);
insert into siblingsT2 values(20,null);
insert into siblingsT2 values(21, 20);
insert into siblingsT2 values(22, 20);
insert into siblingsT2 values(23, 21);
insert into siblingsT2 values(24, 21);
commit;
下記のorder siblings byを使った、Oracle11gR2のSQLと同じ結果を取得する。
-- 模倣対象のOracle11gR2のSQL
col path for a20
select connect_by_root ID as treeID,
ID,OyaID,Level,sys_connect_by_path(to_char(ID),',') as path
from siblingsT2
start with OyaID is null
connect by prior ID = OyaID
order siblings by ID desc;
treeID ID OyaID Level path
------ -- ----- ----- ---------
20 20 null 1 ,20
20 22 20 2 ,20,22
20 21 20 2 ,20,21
20 24 21 3 ,20,21,24
20 23 21 3 ,20,21,23
1 1 null 1 ,1
1 4 1 2 ,1,4
1 8 4 3 ,1,4,8
1 7 4 3 ,1,4,7
1 10 7 4 ,1,4,7,10
1 3 1 2 ,1,3
1 6 3 3 ,1,3,6
1 9 6 4 ,1,3,6,9
1 5 3 3 ,1,3,5
1 2 1 2 ,1,2
-- sample23
with recursive tmp as(
select ID,OyaID,
Row_Number() over(order by ID desc) as rn
from siblingsT2),
rec(ID,OyaID,path,sortArray) as(
select ID,OyaID,array[ID],array[rn]
from tmp
where OyaID is null
union all
select b.ID,b.OyaID,a.path || b.ID,
a.sortArray || b.rn
from rec a,tmp b
where a.ID = b.OyaID)
select path[1] as treeID,ID,OyaID,
array_length(path,1) as LV,
',' || array_to_string(path, ',') as path
from rec
order by sortArray;
Oracleの階層問い合わせのorder siblings byと、
Oracleの再帰with句のsearch句 (深さ優先探索)は、ほぼ同じ機能であるので、
PostgreSQLで模倣する方法は、
17. Oracleのsearch句 (深さ優先探索)を模倣する方法とほぼ同じとなります。
22. connect_by_IsLeaf擬似列
create table IsLeafT(
ID integer primary key,
OyaID integer);
insert into IsLeafT values( 1,null);
insert into IsLeafT values( 2, 1);
insert into IsLeafT values( 3, 2);
insert into IsLeafT values( 4, 3);
insert into IsLeafT values( 5, 1);
insert into IsLeafT values( 6, 5);
insert into IsLeafT values( 7, 2);
insert into IsLeafT values(20,null);
insert into IsLeafT values(21, 20);
insert into IsLeafT values(22, 21);
commit;
下記のconnect_by_IsLeaf擬似列を使った、Oracle11gR2のSQLと同じ結果を取得する。
-- 模倣対象のOracle11gR2のSQL
col path for a20
select ID,OyaID,Level,sys_connect_by_path(to_char(ID),',') as Path,
connect_by_IsLeaf as IsLeaf
from IsLeafT
start with OyaID is null
connect by prior ID = OyaID;
ID OyaID Level Path IsLeaf
-- ----- ----- --------- ------
1 null 1 ,1 0
2 1 2 ,1,2 0
3 2 3 ,1,2,3 0
4 3 4 ,1,2,3,4 1
7 2 3 ,1,2,7 1
5 1 2 ,1,5 0
6 5 3 ,1,5,6 1
20 null 1 ,20 0
21 20 2 ,20,21 0
22 21 3 ,20,21,22 1
-- sample24 exists述語を使用
with recursive rec(ID,OyaID,LV,path) as(
select ID,OyaID,1,array[ID]
from IsLeafT
where OyaID is null
union all
select b.ID,b.OyaID,a.LV+1,a.path || b.ID
from rec a,IsLeafT b
where a.ID = b.OyaID)
select ID,OyaID,LV,',' || array_to_string(path,',') as path,
case when exists(select 1 from IsLeafT b
where a.ID = b.OyaID)
then 0 else 1 end as IsLeaf
from rec a
order by path;
-- sample25 (深さ優先探索の行きがけ順でレベルを比較)
with recursive rec(ID,OyaID,LV,path) as(
select ID,OyaID,1,array[ID]
from IsLeafT
where OyaID is null
union all
select b.ID,b.OyaID,a.LV+1,a.path || b.ID
from rec a,IsLeafT b
where a.ID = b.OyaID)
select ID,OyaID,LV,
',' || array_to_string(path,',') as path,
case when LV < Lead(LV) over(order by path)
then 0 else 1 end as IsLeaf
from rec;
探索木の経路を配列型に記憶させておいてから、Lead関数のソートキーとして使用し、
深さ優先探索の行きがけ順で、次の訪問でレベルがインクリメントされたら葉ではない
と判断してます。
23. connect by noCycle指定,connect_by_IsCycle擬似列
create table noCycleT(
ID integer primary key,
nextID integer);
insert into noCycleT values(1,2);
insert into noCycleT values(2,3);
insert into noCycleT values(3,4);
insert into noCycleT values(4,1);
insert into noCycleT values(5,5);
insert into noCycleT values(7,8);
insert into noCycleT values(8,7);
commit;
下記のconnect by noCycle指定とconnect_by_IsCycle擬似列を使った、
Oracle11gR2のSQLと同じ結果を取得する。
-- 模倣対象のOracle11gR2のSQL
col path for a10
select ID,nextID,
sys_connect_by_path(to_char(ID),',') as path,
connect_by_IsCycle as IsCycle
from noCycleT
start with ID in(1,5,7)
connect by noCycle prior nextID = ID;
ID nextID path IsCycle
-- ------ -------- -------
1 2 ,1 0
2 3 ,1,2 0
3 4 ,1,2,3 0
4 1 ,1,2,3,4 1
5 5 ,5 1
7 8 ,7 0
8 7 ,7,8 1
-- sample26
with recursive rec(ID,nextID,path) as(
select ID,nextID,array[ID]
from noCycleT
where ID in(1,5,7)
union all
select b.ID,b.nextID,a.path || b.ID
from rec a,noCycleT b
where a.nextID = b.ID
and b.ID != all(a.path))
select ID,nextID,
',' || array_to_string(path,',') as path,
case when exists(select 1 from rec b
where a.path[1] = b.path[1]
and a.nextID = b.ID
and b.ID = any(a.path))
then 1 else 0 end as IsCycle
from rec a
order by path;
同じ木で親子条件を満たして、かつ、訪問済なノードが存在するかを
exists述語でチェックして、connect_by_IsCycle擬似列を模倣してます。
Oracleの階層問い合わせのconnect by noCycle指定,connect_by_IsCycle擬似列と、
Oracleの再帰with句のcycle句は、似た機能であるので、
PostgreSQLで模倣する方法は、
19. Oracleのcycle句を模倣する方法と似ています。
第6部 再帰SQLの実践編
24. リセット機能付の累計
OracleSQLパズル 10-303 リセット機能付の累計より
create table resetRunSum(SK,Val) as
values( 1, 0),
( 3, 10),
( 5, 20),
( 6,-15),
( 7,-20),
( 8, 10),
(10, 5),
(13, 50),
(16, 15),
(20, 0),
(21,-10),
(32,-30),
(33,-40),
(46,100),
(48,-20),
(66, 40),
(67, 35),
(89, 20),
(90, 10);
SKをソートキーとしてのValの累計を求める。
ただし、累計がプラスならリセットして0とする。
また、累計がマイナスなら0として表示する。
出力結果
SK Val runSum
-- --- ------
1 0 0
3 10 10
5 20 20
6 -15 0 -15
7 -20 0 -35 (-15-20)
8 10 0 -25 (-15-20+10)
10 5 0 -20 (-15-20+10+5)
13 50 30 30 (-15-20+10+5+50)
16 15 15
20 0 0
21 -10 0 -10
32 -30 0 -40 (-10-30)
33 -40 0 -80 (-10-30-40)
46 100 20 20 (-10-30-40+100)
48 -20 0 -20
66 40 20 20 (-20+40)
67 35 35
89 20 20
90 10 10
-- sample27
with recursive tmp as(
select SK,Val,Row_Number() over(order by SK) as rn
from resetRunSum),
rec(SK,Val,runSum,rn) as(
select SK,Val,Least(0,Val),rn
from tmp
where rn=1
union all
select b.SK,b.Val,Least(0,a.runSum)+b.Val,b.rn
from rec a,tmp b
where a.rn+1=b.rn)
select SK,Val,greatest(0,runSum) as runSum
from rec;
再帰SQLで、その行の1行前までの合計を順に求めつつ、
Least関数で、累計がプラスならリセットして0にしてます。
マニュアル --- 9.16.4. GREATESTおよびLEAST
25. 部下一覧の作成
OracleSQLパズル 7-80 階層問い合わせで部下一覧を作成より
create table 組織(役職,上司) as
values('社長',null ),
('課長','社長'),
('平1' ,'課長'),
('平2' ,'課長');
下記の部下一覧を作成する。
部下が1人もいない場合は、部下をnullとして表示する。
出力結果
役職 部下
---- ----
社長 課長
社長 平1
社長 平2
課長 平1
課長 平2
平1 null
平2 null
-- sample28
with recursive rec(root役職,役職,上司,LV) as(
select 役職,役職,上司,1
from 組織
union all
select a.root役職,b.役職,b.上司,a.LV+1
from rec a,組織 b
where a.役職 = b.上司)
select root役職,nullif(役職,root役職) as 部下
from (select count(*) over(partition by root役職) as cnt,
root役職,役職,LV
from rec) a
where cnt = 1 or LV > 1
order by cnt desc,root役職,LV,部下;
window関数のcount関数で木ごとのノード数を求めて、
ノード数が1であるか、ノードのレベルが1であることを
where句で指定してます。
26. 迷路問題
OracleSQLパズル 10-317 階層問い合わせで迷路問題を解くより
create table matrix(ID,A,B,C,D,E,F,G,H,I,J) AS
values('A',1,1,1,0,0,0,1,0,1,0),
('B',0,0,0,0,1,1,1,0,1,0),
('C',0,1,1,1,1,0,0,0,0,1),
('D',1,0,0,0,1,0,1,0,0,0),
('E',1,1,0,0,0,0,0,0,0,1),
('F',0,1,1,0,1,1,0,0,0,0),
('G',0,1,0,1,1,1,0,1,0,1),
('H',1,1,0,1,0,0,0,1,0,0),
('I',0,1,1,1,0,1,1,1,0,1),
('J',1,0,0,0,0,0,0,1,0,1),
('K',1,0,0,1,1,1,0,1,1,0),
('L',0,0,1,0,1,1,0,0,1,0),
('M',0,0,1,0,0,0,0,1,1,1),
('N',1,0,1,0,0,0,1,1,1,0),
('O',1,0,0,1,1,0,1,0,0,0);
matrixテーブル
ID A B C D E F G H I J
-- - - - - - - - - - -
A 1 1 1 0 0 0 1 0 1 0
B 0 0 0 0 1 1 1 0 1 0
C 0 1 1 1 1 0 0 0 0 1
D 1 0 0 0 1 0 1 0 0 0
E 1 1 0 0 0 0 0 0 0 1
F 0 1 1 0 1 1 0 0 0 0
G 0 1 0 1 1 1 0 1 0 1
H 1 1 0 1 0 0 0 1 0 0
I 0 1 1 1 0 1 1 1 0 1
J 1 0 0 0 0 0 0 1 0 1
K 1 0 0 1 1 1 0 1 1 0
L 0 0 1 0 1 1 0 0 1 0
M 0 0 1 0 0 0 0 1 1 1
N 1 0 1 0 0 0 1 1 1 0
O 1 0 0 1 1 0 1 0 0 0
ID=Aの行のE列を出発点として、ID=Oの行までの経路を求める。
ただし、0と1を交互に訪問しなければならない。
出力結果
PATH
--------------------------------------------------------------------------------
[A,E];[B,E];[B,D];[C,D];[D,D];[D,E];[D,F];[D,G];[C,G];[B,G];[B,H];[B,I];[B,J];
[C,J];[D,J];[E,J];[F,J];[G,J];[G,I];[G,H];[G,G];[G,F];[H,F];[I,F];[J,F];[K,F];
[K,G];[K,H];[L,H];[L,I];[L,J];[M,J];[N,J];[N,I];[O,I]
[A,E];[B,E];[B,D];[C,D];[D,D];[D,E];[D,F];[D,G];[C,G];[B,G];[B,H];[B,I];[C,I];
[C,J];[D,J];[E,J];[F,J];[G,J];[G,I];[G,H];[G,G];[G,F];[H,F];[I,F];[J,F];[K,F];
[K,G];[K,H];[L,H];[L,I];[L,J];[M,J];[N,J];[N,I];[O,I]
-- sample29
with recursive tmp(ID,X,Val) as(
select a.ID,
case b.cnt when 1 then 'A' when 2 then 'B'
when 3 then 'C' when 4 then 'D'
when 5 then 'E' when 6 then 'F'
when 7 then 'G' when 8 then 'H'
when 9 then 'I' when 10 then 'J' end,
case b.cnt when 1 then a.A when 2 then a.B
when 3 then a.C when 4 then a.D
when 5 then a.E when 6 then a.F
when 7 then a.G when 8 then a.H
when 9 then a.I when 10 then a.J end
from matrix a,generate_series(1,10) as b(cnt)),
rec(ID,X,Val,Path,OutPath) as(
select ID,X,Val,array[row(ID,X)],
'[' || ID || ',' || X || ']'
from tmp
where ID='A' and X = 'E'
union all
select b.ID,b.X,b.Val,a.Path || row(b.ID,b.X),
a.OutPath || ';[' || b.ID || ',' || b.X || ']'
from rec a,tmp b
where (b.ID,b.X) in((chr(ascii(a.ID)+1),a.X),
(chr(ascii(a.ID)-1),a.X),
(a.ID,chr(ascii(a.X)+1)),
(a.ID,chr(ascii(a.X)-1)))
and row(b.ID,b.X) !=all(a.Path)
and a.ID != 'O'
and (a.Val = 1 and b.Val=0
or a.Val = 0 and b.Val=1))
select OutPath from rec
where ID='O';
27. 碁石の固まり
OracleSQLパズル 8-26 碁石の固まりを出力より
create table goishi(Color,X,Y) as
values('Black','B',1),
('Black','B',2),
('Black','B',3),
('Black','B',4),
('Black','B',5),
('Black','C',4),
('Black','D',5),
('Black','E',4),
('Black','F',3),
('Black','F',4),
('Black','F',5),
('Black','G',4),
('White','C',2),
('White','D',2),
('White','D',3),
('White','D',4),
('White','F',1),
('White','F',2),
('White','G',2);
ＡＢＣＤＥＦＧ
１┳●┳┳┳○┓
２╋●○○╋○○
３╋●╋○╋●┫
４╋●●○●●●
５╋╋╋●╋●┫
碁石のつながり情報を示す連番を付与して出力する。
出力結果
GID Color X Y
--- ----- -- --
1 Black B 1
1 Black B 2
1 Black B 3
1 Black B 4
1 Black B 5
1 Black C 4
2 Black D 5
3 Black E 4
3 Black F 3
3 Black F 4
3 Black F 5
3 Black G 4
1 White C 2
1 White D 2
1 White D 3
1 White D 4
2 White F 1
2 White F 2
2 White G 2
-- sample30
with recursive rec(rootColor,rootX,rootY,X,Y,path) as(
select Color,X,Y,X,Y,array[row(X,Y)]
from goishi
union all
select a.rootColor,a.rootX,a.rootY,b.X,b.Y,a.path || row(b.X,b.y)
from rec a,goishi b
where a.rootColor = b.Color
and (b.X,b.Y) in((a.X,a.Y+1),
(a.X,a.Y-1),
(chr(ascii(a.X)+1),a.Y),
(chr(ascii(a.X)-1),a.Y))
and row(b.X,b.Y) != all(a.path))
select dense_rank() over(partition by rootColor order by min(X),min(Y)) as GID,
rootColor,rootX,rootY
from rec
group by rootColor,rootX,rootY
order by rootColor,rootX,rootY;
再帰SQLで訪問可能なノードを全て列挙しつつ、
dense_rank関数で、訪問可能なノードで順序付けして連番を付与してます。
28. Uniqな時間にインクリメント
OracleSQLパズル 10-320 ユニークな時間にインクリメントしてselectより
create table MakeUniqVal(ID,Val) as
values('01',TimeStamp '2010-10-12 10:10:00'),
('01',TimeStamp '2010-10-12 10:10:00'),
('01',TimeStamp '2010-10-12 10:10:00'),
('01',TimeStamp '2010-10-12 10:11:00'),
('01',TimeStamp '2010-10-12 10:30:00'),
('01',TimeStamp '2010-10-12 10:30:00'),
('01',TimeStamp '2010-10-12 10:30:00'),
('02',TimeStamp '2010-10-12 10:10:00'),
('02',TimeStamp '2010-10-12 10:10:00');
MakeUniqVal
ID Val
-- ----------------
01 2010-10-12 10:10
01 2010-10-12 10:10
01 2010-10-12 10:10
01 2010-10-12 10:11
01 2010-10-12 10:30
01 2010-10-12 10:30
01 2010-10-12 10:30
02 2010-10-12 10:10
02 2010-10-12 10:10
ValがIDごとでユニークになるように、1分単位でインクリメントする。
出力結果
ID Val
-- ----------------
01 2010/10/12 10:10
01 2010/10/12 10:11
01 2010/10/12 10:12
01 2010/10/12 10:13
01 2010/10/12 10:30
01 2010/10/12 10:31
01 2010/10/12 10:32
02 2010/10/12 10:10
02 2010/10/12 10:11
-- sample31
with recursive tmp as(
select ID,Val,
Row_Number() over(partition by ID order by Val) as rn
from MakeUniqVal),
rec(ID,Val,rn) as(
select ID,Val,rn
from tmp
where rn=1
union all
select b.ID,greatest(a.Val+InterVal '1' minute,b.Val),b.rn
from rec a,tmp b
where a.ID = b.ID
and a.rn+1=b.rn)
select ID,Val
from rec
order by ID,Val;
最初にRow_Number関数を使って、Valの昇順な連番を付与しておいてから、
再帰SQLを使って連番の順序でValを確定させてます。