OracleSQLパズル
明智重蔵のブログ
明智重蔵のTwitter
記事(CodeZine)
DB2 SQLパズル
SQL徹底指南書の前半問題をDB2で解く
概要
Club DB2の「第108回 【SQL上級編2】 DB2でSQL徹底指南書の問題を解く」で、
私が講師をさせていただきまして、そのまとめページです。
達人に学ぶ SQL徹底指南書の前半問題から
分析関数や再帰SQLが効果的な問題をピックアップして、DB2 V9.7で解きつつ、
私のSQLの思考法と脳内のイメージを解説しました。
プログラム
1. 重複行を削除する (32ページ)
create table Products(name varchar(9),price integer);
insert into Products values('りんご', 50),
('みかん',100),
('みかん',100),
('みかん',100),
('バナナ', 80);
delete文で、重複行を1行にします。
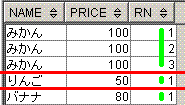
削除結果
name price
------ -----
りんご 50
みかん 100
バナナ 80
重複行を1行にしたい、といった質問は、US-OTNでよく見かけます。
DB2の分析関数の使用例 20. delete文で重複行を削除で扱ったように、
分析関数を使用した削除可能なビュー(DeletableView)を使ってdeleteすれば、重複行を削除できます。
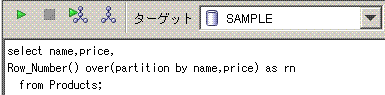
-- Sample1
delete from (select Row_Number() over(partition by name,price) as rn
from Products)
where rn > 1;
Row_Number関数でorder byを省略すると、テキトーなソートで連番を付与しますが、
この場合は、テキトーなソートでも困りません。
■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
脳内のイメージは、下記となります。partition by name,priceに対応する赤線を引いてから、
Row_Number関数で付与する連番に対応する黄緑線を引いてます。
2. 部分的に不一致なキーの検索 (34ページ)
create table Addresses(Name varchar(15),family_ID integer,address varchar(18) not null);
insert into Addresses values('前田 義明',100,'3-2-29'),
('前田 由美',100,'3-2-92'),
('加藤 茶' ,200,'2-8-1'),
('加藤 勝' ,200,'2-8-1'),
('ホームズ' ,300,'221B'),
('ワトソン' ,400,'221B');
family_IDが同じだが、addressが異なるレコードを出力します。
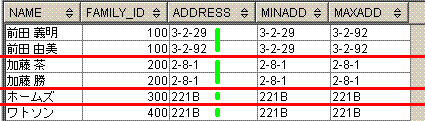
出力結果
Name address
--------- -------
前田 義明 3-2-29
前田 由美 3-2-92
DB2の分析関数の使用例 21. count(distinct Val) over(partition by ID)
で扱ったように、Oracleなら分析関数のcount関数でdistinctオプションが使えるのですが、DB2 V9.7では、使えないので、
dense_rank関数で付けた順位の最大値を求めて代用したのが、下記のSQLです。
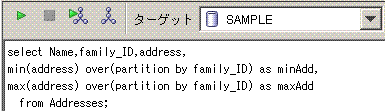
-- Sample2
select Name,address
from (select Name,address,
max(Rn) over(partition by family_ID) as maxRn
from (select Name,address,family_ID,
dense_rank() over(partition by family_ID order by address) as Rn
from Addresses))
where maxRn > 1;
最大値と最小値が異なればユニークでない。といった考え方を使った、下記のSQLでもいいです。
-- Sample3
select Name,address
from (select Name,address,
min(address) over(partition by family_ID) as minAdd,
max(address) over(partition by family_ID) as maxAdd
from Addresses)
where minAdd != maxAdd;
■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
脳内のイメージは、下記となります。partition by family_IDに対応する赤線を引き、
min(address)とmax(address)に対応する黄緑線を引いてます。
 ■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
分析関数を使わないで同じ結果を取得するのであれば、下記のexists述語を使ったSQLとなります。
-- Sample4
select Name,address
from Addresses a
where exists(select 1 from Addresses b
where a.family_ID = b.family_ID
and a.address != b.address);
■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
分析関数を使わないで同じ結果を取得するのであれば、下記のexists述語を使ったSQLとなります。
-- Sample4
select Name,address
from Addresses a
where exists(select 1 from Addresses b
where a.family_ID = b.family_ID
and a.address != b.address);
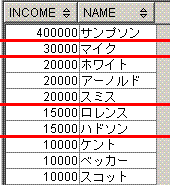
3. 最頻値を求める (67ページ)
create table Graduates(name varchar(15),income integer);
insert into Graduates values('サンプソン',400000),
('マイク', 30000),
('ホワイト', 20000),
('アーノルド', 20000),
('スミス', 20000),
('ロレンス', 15000),
('ハドソン', 15000),
('ケント', 10000),
('ベッカー', 10000),
('スコット', 10000);
incomeの最頻値(モード)を求めます。
出力結果
income cnt
------ ---
10000 3
20000 3
-- Sample5
select income,cnt
from (select income,count(*) as cnt,
max(count(*)) over() as maxCnt
from Graduates
group by income)
where cnt = maxCnt;
慣れないと分かりにくいのですが、分析関数のmax関数の引数に、集約関数のcount関数を使用してます。
DB2の分析関数の使用例 13. 最頻値(モード)でも同じことを行ってますね。
■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
脳内のイメージは、下記となります。group by incomeに対応する赤線を引いてます。
 ■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
分析関数を使わないで同じ結果を取得するのであれば、下記のall述語を使ったSQLとなります。
-- Sample6
select income,count(*) as cnt
from Graduates
group by income
having count(*) >= all(select count(*)
from Graduates
group by income);
■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
分析関数を使わないで同じ結果を取得するのであれば、下記のall述語を使ったSQLとなります。
-- Sample6
select income,count(*) as cnt
from Graduates
group by income
having count(*) >= all(select count(*)
from Graduates
group by income);
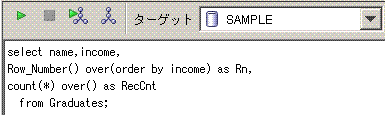
4. メジアンを求める (70ページ)
前問は、incomeの最頻値(モード)を求めましたが、
今度は、incomeの中央値(メジアン)を求めます。
出力結果
MedianVal
---------
17500
-- Sample7
select avg(income) as MedianVal
from (select name,income,
count(*) over() as RecCnt,
Row_Number() over(order by income) as Rn
from Graduates)
where mod(RecCnt,2) = 0 and Rn in(RecCnt/2,RecCnt/2+1)
or mod(RecCnt,2) = 1 and Rn = Ceil(RecCnt/2.0);
DB2の分析関数の使用例 28. 中央値(メジアン)を求めると同じ考え方で、
インラインビューで、分析関数のcount関数でレコード数を求めて、Row_Number関数で順位を求めて、
where句でレコード数が偶数か奇数かで場合分けしてます。
■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
脳内のイメージは、下記となります。
Row_Number() over(order by income)とcount(*) over()に対応する黄緑線を引いてます。
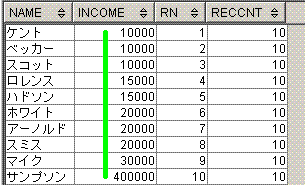 ■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
下記の、データ件数が奇数の場合と、偶数の場合の
正順位と逆順位の差をふまえた下記のSQLでもメジアンを求めることができます。
データ件数が5件(奇数)の場合
正順位 1 2 3 4 5
逆順位 5 4 3 2 1
差 4 2 0 2 4
データ件数が4件(偶数)の場合
正順位 1 2 3 4
逆順位 4 3 2 1
差 3 1 1 3
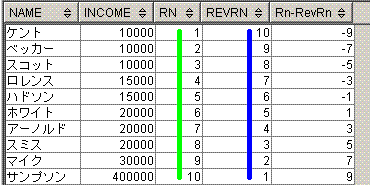
-- Sample8
select avg(income) as MedianVal
from (select name,income,
Row_Number() over(order by income) as Rn,
Row_Number() over(order by income desc) as RevRn
from Graduates)
where Rn-RevRn in (-1,0,1);
■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
脳内のイメージは、下記となります。
Row_Number() over(order by income)に対応する黄緑線を引き、
Row_Number() over(order by income desc)に対応する青線を引いてます。
■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
下記の、データ件数が奇数の場合と、偶数の場合の
正順位と逆順位の差をふまえた下記のSQLでもメジアンを求めることができます。
データ件数が5件(奇数)の場合
正順位 1 2 3 4 5
逆順位 5 4 3 2 1
差 4 2 0 2 4
データ件数が4件(偶数)の場合
正順位 1 2 3 4
逆順位 4 3 2 1
差 3 1 1 3
-- Sample8
select avg(income) as MedianVal
from (select name,income,
Row_Number() over(order by income) as Rn,
Row_Number() over(order by income desc) as RevRn
from Graduates)
where Rn-RevRn in (-1,0,1);
■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
脳内のイメージは、下記となります。
Row_Number() over(order by income)に対応する黄緑線を引き、
Row_Number() over(order by income desc)に対応する青線を引いてます。

5. 直近と比較 (108ページ)
create table Sales2(Nen integer not null primary key,sale integer);
insert into Sales2 values(1990,50),
(1992,50),
(1993,52),
(1994,55),
(1997,55);
Nenをソートキーとして、前の行とsaleが等しい行を出力します。
いいかえれば、Nenをソートキーとして、最大下界の行とsaleが等しい行を出力します。
出力結果
Nen sale
---- ----
1992 50
1997 55
DB2の分析関数の使用例 7. 前後の値で扱ったように、
指定したソートキーでの、前の行の値が欲しい時には、Lag関数が使えます。
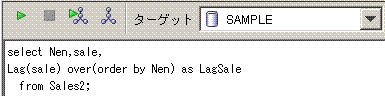
-- Sample9
select Nen,sale
from (select Nen,sale,
Lag(sale) over(order by Nen) as LagSale
from Sales2)
where sale = LagSale;
■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
脳内のイメージは、下記となります。
Lag(sale) over(order by Nen)に対応する黄緑線を引いてます。
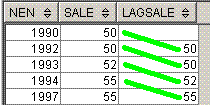 ■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
分析関数を使わないで同じ結果を取得するのであれば、
下記の、相関サブクエリでfetch first句を使ったSQLとなります。
-- Sample10
select Nen,sale
from Sales2 a
where sale = (select b.sale
from Sales2 b
where b.Nen < a.Nen
order by b.Nen desc
fetch first 1 rows only);
■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
分析関数を使わないで同じ結果を取得するのであれば、
下記の、相関サブクエリでfetch first句を使ったSQLとなります。
-- Sample10
select Nen,sale
from Sales2 a
where sale = (select b.sale
from Sales2 b
where b.Nen < a.Nen
order by b.Nen desc
fetch first 1 rows only);
第2部 SQLで集合演算
6. 集合の相等性チェック (124ページ)
create table Tbl_A(
keycol char(1) not null primary key,
col_1 integer,
col_2 integer,
col_3 integer);
create table Tbl_B(
keycol char(1) not null primary key,
col_1 integer,
col_2 integer,
col_3 integer);
-- case1 テーブル同士が等しい
delete from Tbl_A;
delete from Tbl_B;
insert into Tbl_A values('A', 2, 3, 4),('B', 0, 7, 9),('C', 5, 1, 6);
insert into Tbl_B values('A', 2, 3, 4),('B', 0, 7, 9),('C', 5, 1, 6);
-- case2 キーが「B」の行の値が違う
delete from Tbl_A;
delete from Tbl_B;
insert into Tbl_A values('A', 2, 3, 4),('B', 0, 7, 9),('C', 5, 1, 6);
insert into Tbl_B values('A', 2, 3, 4),('B', 0, 7, 8),('C', 5, 1, 6);
同じ定義のTbl_AとTbl_Bのデータが同じかを確認します。
-- Sample11
select a.*,count(*) over()
from Tbl_A a
except all
select a.*,count(*) over()
from Tbl_B a;
DB2の分析関数の使用例 3. except allとcount(*) over()で扱ったように、
2つのselect文の結果が同じか確認するときや、同じ定義の2テーブルのデータが同じか確認する時に使えるのが、
except allとcount(*) over() の組み合わせです。
上記のselect文の結果が0件になるのは、以下の少なくとも1つが成り立つ場合です。
・Tbl_Aが空集合(レコードが0件)
・Tbl_AとTbl_Bのデータが同じ
実際の業務において、空集合ということは、まずないので
上記のselect文の結果が0件なら、Tbl_AとTbl_Bのデータが同じと判定できます。
■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
数学の集合では、集合の相等性を調べる公式として、以下が有名ですが、
(A ⊆ B ) かつ (A ⊇ B) ⇔ (A = B)
(集合Aと集合Bの要素数が等しい) かつ (A ⊆ B) ⇔ (A = B) も成立します。
集合Aと集合Bが両方とも空集合の場合は、自明ですし、
集合Aと集合Bが両方とも空集合でない場合は、要素数が等しくて包含関係が成立するのは、A=Bの場合しかないからです。
要素数は、分析関数のcount関数を使えば求まりますし、
包含関係は、差集合が空集合かどうかを調べれば分かります。
7. 関係除算 (129ページ)
create table Skills(skill varchar(18) not null primary key);
insert into Skills values('Oracle'),
('UNIX'),
('Java');
create table EmpSkills(
emp varchar(6) not null,
skill varchar(18) not null,
primary key(emp, skill));
insert into EmpSkills values('相田','Oracle'),
('相田','UNIX'),
('相田','Java'),
('相田','C#'),
('神崎','Oracle'),
('神崎','UNIX'),
('神崎','Java'),
('平井','UNIX'),
('平井','Oracle'),
('平井','PHP'),
('平井','Perl'),
('平井','C++'),
('若田','Perl'),
('渡来','Oracle');
EmpSkillsテーブルから、
Skillsテーブルの全てのskill(Oracle,UNIX,Java)を持つ人を出力します。
出力結果
emp
----
相田
神崎
-- Sample12
select b.emp
from (select skill,count(*) over() as cnt
from Skills) a
Join EmpSkills b
on a.skill = b.skill
group by b.emp,a.cnt
having count(*) = a.cnt;
最初にインラインビューで分析関数のcount関数を使って、
Skillsテーブルの行数を列別名cntとして求めてます。
次に、skillが等しいことを条件として内部結合(等価結合)してます。
そして、group by b.emp,a.cntでグループ化し、having count(*) = a.cntによって、
内部結合した結果の件数がSkillsテーブルの行数と同じであることを抽出条件としてます。
脳内のイメージは、下記となります。
分析関数のcount関数に対応する黄緑線を引き、
skillが等しいことを条件とした内部結合(等価結合)に対応するベン図をイメージしながら青線や紫線などを引き、
group by b.emp,a.cntに対応する赤線を引いてます。
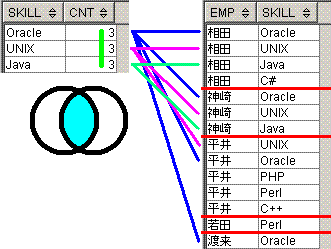
8. 等しい部分集合を見つける (132ページ)
create table SupParts(sup char(2),part varchar(12));
insert into SupParts values('A','ボルト'),
('A','ナット'),
('A','パイプ'),
('B','ボルト'),
('B','パイプ'),
('C','ボルト'),
('C','ナット'),
('C','パイプ'),
('D','ボルト'),
('D','パイプ'),
('E','ヒューズ'),
('E','ナット'),
('E','パイプ'),
('F','ヒューズ');
数も種類もまったく同じpartを取り扱うsupの組み合わせを求めます。
出力結果
s1 s2
-- --
A C
B D
-- Sample13
with tmp as(
select sup,part,count(*) over(partition by sup) as cnt
from SupParts)
select a.sup as s1,b.sup as s2
from tmp a,tmp b
where a.sup < b.sup
and a.cnt = b.cnt
and a.part = b.part
group by a.sup,b.sup,a.cnt
having count(*) = a.cnt
order by a.sup,b.sup;
まず、分析関数のcount関数でsupごとの件数を求めた結果を、仮想表tmpとしてます。
次に、supが自分より大きいこと、件数が等しいこと、partが等しいこと
を条件として自己内部結合させてます。
with句は、select文の結果同士を自己結合させる際に使うと便利です。
そして、group by句でsupの組み合わせでグループ化して、
having count(*) = a.cntで、内部結合によって件数が減らなかったsupの組み合わせを出力対象としてます。
脳内のイメージは、下記となります。
仮想表tmpのselect文のcount(*) over(partition by sup)に対応する赤線と黄緑線を引いてから、
仮想表tmp同士の、supが自分より大きいこと、件数が等しいこと、partが等しいこと
を条件とした自己内部結合をイメージしてます。
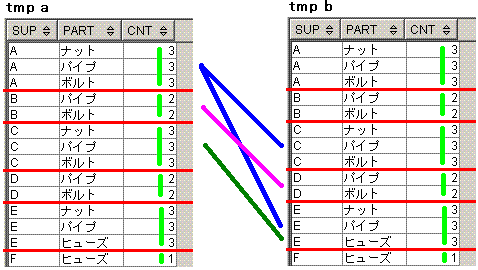 ■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
数学の集合では、集合の相等性を調べる公式として、以下が有名ですが、
(A ⊆ B ) かつ (A ⊇ B) ⇔ (A = B)
(集合Aと集合Bの要素数が等しい) かつ (A ⊆ B) ⇔ (A = B) も成立します。
集合Aと集合Bが両方とも空集合の場合は、自明ですし、
集合Aと集合Bが両方とも空集合でない場合は、要素数が等しくて包含関係が成立するのは、A=Bの場合しかないからです。
要素数は、分析関数のcount関数を使えば求まりますし、
包含関係は、要素が等しいことを条件として内部結合して、要素数が減らなかったかを調べれば分かります。
■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
数学の集合では、集合の相等性を調べる公式として、以下が有名ですが、
(A ⊆ B ) かつ (A ⊇ B) ⇔ (A = B)
(集合Aと集合Bの要素数が等しい) かつ (A ⊆ B) ⇔ (A = B) も成立します。
集合Aと集合Bが両方とも空集合の場合は、自明ですし、
集合Aと集合Bが両方とも空集合でない場合は、要素数が等しくて包含関係が成立するのは、A=Bの場合しかないからです。
要素数は、分析関数のcount関数を使えば求まりますし、
包含関係は、要素が等しいことを条件として内部結合して、要素数が減らなかったかを調べれば分かります。



 ■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
分析関数を使わないで同じ結果を取得するのであれば、下記のexists述語を使ったSQLとなります。
-- Sample4
select Name,address
from Addresses a
where exists(select 1 from Addresses b
where a.family_ID = b.family_ID
and a.address != b.address);
■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
分析関数を使わないで同じ結果を取得するのであれば、下記のexists述語を使ったSQLとなります。
-- Sample4
select Name,address
from Addresses a
where exists(select 1 from Addresses b
where a.family_ID = b.family_ID
and a.address != b.address);
 ■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
分析関数を使わないで同じ結果を取得するのであれば、下記のall述語を使ったSQLとなります。
-- Sample6
select income,count(*) as cnt
from Graduates
group by income
having count(*) >= all(select count(*)
from Graduates
group by income);
■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
分析関数を使わないで同じ結果を取得するのであれば、下記のall述語を使ったSQLとなります。
-- Sample6
select income,count(*) as cnt
from Graduates
group by income
having count(*) >= all(select count(*)
from Graduates
group by income);

 ■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
下記の、データ件数が奇数の場合と、偶数の場合の
正順位と逆順位の差をふまえた下記のSQLでもメジアンを求めることができます。
データ件数が5件(奇数)の場合
正順位 1 2 3 4 5
逆順位 5 4 3 2 1
差 4 2 0 2 4
データ件数が4件(偶数)の場合
正順位 1 2 3 4
逆順位 4 3 2 1
差 3 1 1 3
-- Sample8
select avg(income) as MedianVal
from (select name,income,
Row_Number() over(order by income) as Rn,
Row_Number() over(order by income desc) as RevRn
from Graduates)
where Rn-RevRn in (-1,0,1);
■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
脳内のイメージは、下記となります。
Row_Number() over(order by income)に対応する黄緑線を引き、
Row_Number() over(order by income desc)に対応する青線を引いてます。
■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
下記の、データ件数が奇数の場合と、偶数の場合の
正順位と逆順位の差をふまえた下記のSQLでもメジアンを求めることができます。
データ件数が5件(奇数)の場合
正順位 1 2 3 4 5
逆順位 5 4 3 2 1
差 4 2 0 2 4
データ件数が4件(偶数)の場合
正順位 1 2 3 4
逆順位 4 3 2 1
差 3 1 1 3
-- Sample8
select avg(income) as MedianVal
from (select name,income,
Row_Number() over(order by income) as Rn,
Row_Number() over(order by income desc) as RevRn
from Graduates)
where Rn-RevRn in (-1,0,1);
■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
脳内のイメージは、下記となります。
Row_Number() over(order by income)に対応する黄緑線を引き、
Row_Number() over(order by income desc)に対応する青線を引いてます。



 ■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
分析関数を使わないで同じ結果を取得するのであれば、
下記の、相関サブクエリでfetch first句を使ったSQLとなります。
-- Sample10
select Nen,sale
from Sales2 a
where sale = (select b.sale
from Sales2 b
where b.Nen < a.Nen
order by b.Nen desc
fetch first 1 rows only);
■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
分析関数を使わないで同じ結果を取得するのであれば、
下記の、相関サブクエリでfetch first句を使ったSQLとなります。
-- Sample10
select Nen,sale
from Sales2 a
where sale = (select b.sale
from Sales2 b
where b.Nen < a.Nen
order by b.Nen desc
fetch first 1 rows only);

 ■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
数学の集合では、集合の相等性を調べる公式として、以下が有名ですが、
(A ⊆ B ) かつ (A ⊇ B) ⇔ (A = B)
(集合Aと集合Bの要素数が等しい) かつ (A ⊆ B) ⇔ (A = B) も成立します。
集合Aと集合Bが両方とも空集合の場合は、自明ですし、
集合Aと集合Bが両方とも空集合でない場合は、要素数が等しくて包含関係が成立するのは、A=Bの場合しかないからです。
要素数は、分析関数のcount関数を使えば求まりますし、
包含関係は、要素が等しいことを条件として内部結合して、要素数が減らなかったかを調べれば分かります。
■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■
数学の集合では、集合の相等性を調べる公式として、以下が有名ですが、
(A ⊆ B ) かつ (A ⊇ B) ⇔ (A = B)
(集合Aと集合Bの要素数が等しい) かつ (A ⊆ B) ⇔ (A = B) も成立します。
集合Aと集合Bが両方とも空集合の場合は、自明ですし、
集合Aと集合Bが両方とも空集合でない場合は、要素数が等しくて包含関係が成立するのは、A=Bの場合しかないからです。
要素数は、分析関数のcount関数を使えば求まりますし、
包含関係は、要素が等しいことを条件として内部結合して、要素数が減らなかったかを調べれば分かります。